Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 13.Problemas - Ex. 17

Em uma amostra de 500 famílias da cidade A, constatou-se que 298 haviam comprado,

durante os últimos 30 dias, o refrigerante Meca-Mela em sua nova versão incolor. Na

cidade B esse número foi de 147 em 300 famílias entrevistadas. Na cidade A foi feita uma

campanha publicitária através da rádio local, e não na cidade B. Os resultados trazem

evidências de que as campanhas locais aumentam as vendas?

Passo 1

  Começamos definindo a variável X   =   c o n s u m o   d e   r e f r i g e r a n t e   e m   30   d i a s .

Do enunciado, temos o seguinte:

p ^ A = 298 500 = 0,596

p ^ B = 147 300 = 0,49

Supondo que as popualçoes seguem uma distribuição normal e são independentes, e considerando α = 5 % .

Temos de realizar o teste de hipótese para a diferença entre as proporções de famílias que consumiram o refrigerante:

Teste de Hipótese: H 0 : p A - p B = ∆ 0 = 0   e       H 1 : p A - p B > 0

Como: ∆ 0 = 0 sob H 0 utilizamos a seguinte aproximação:

Z = p ^ A - p ^ B p ^ t 1 - p ^ t 1 n A + 1 n B ~ N 0,1

Onde:

p ^ t = 298 + 147 500 + 300 = 0,556

Passo 2

Construção da Região Crítica: R C = z 0 ∈ R z 0 > z α

Como nossa hipótese alternativa apresenta o sinal de “>”, devemos buscar somente o limite superior na tabela de distribuição normal.

Então: z 0,05 = 1,64

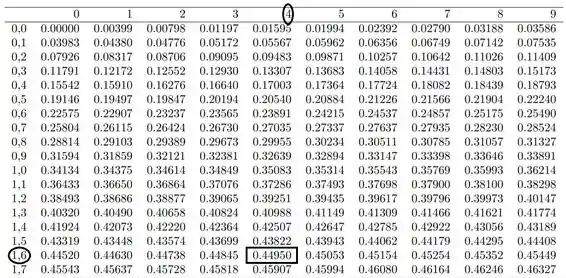
Portanto nossa região crítica assume a seguinte forma:

R C = z 0 > 1,64

Passo 3

Teste sob H 0 :

z 0 = 0,596 - 0,49 0,556   .   0,444   .   1 500 + 1 300 = 2,92

Resposta

Como, z 0 = 2,92 ∈ R C , devemos rejeitar H 0 e temos evidencias de que a proporção de famílias que tomaram refrigerante nos últimos 30 dias é maior na cidade A , onde foi feita uma campanha publicitária através da rádio local, concluímos que as campanhas locais aumentam as vendas.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Testar a hipótese de igualdade das médias populacionais, ao nível de significância de 10 % , admitindo que as variâncias populacionais são diferentes, para os dados dos exercícios:a) 19 b) 18
De uma população animal escolheu-se uma amostra de 10 cobaias, tais cobaias foram submetidas ao tratamento com uma ração especial por um mês; na tabela a seguir estão mostrados os pesos antes ( X i )
Dados: n 1 = 25 , X 1 - = 8 , S 1 = 1,58 , f 1 = 60 % para uma certa população e, para outra população: n 2 = 31 , X 2 - = 7 , S 2 = 1,24 , f 2 = 35 % , testar:a) H 0 : μ 1 = 7,5H 1 : μ 17,5 α = 5 % b
Testar se o nascimento de homens e mulheres é igualmente provável, se em uma pesquisa com 120 famílias de 4 crianças, escolhidas ao acaso, revelou ( α = 0,05 ):
Uma empresa está estudando duas marcas de pneus A e B. Testou 11 pneus de cada marca, quanto a durabilidade, e constatou: para a marca A um média de 23.600 km e um desvio padrão de 3.200 km, e, para a