Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 13.Problemas - Ex. 16

Para investigar a lealdade de consumidores a um determinado produto, sorteou-se uma amostrade 200 homens e 200 mulheres. Foram classificados como tendo alto grau de fidelidade 100homens e 120 mulheres. Os dados trazem evidências de diferença de grau de fidelidade entreos sexos? Em caso afirmativo construa um intervalo de confiança para a diferença.

Passo 1

Definindo a variável X =   g r a u   d e   f i d e l i d a d e

Do enunciado, temos:

p ^ h = 100 200 = 0,5

p ^ m = 120 200 = 0,6

Considerando duas populações com distribuição normal e independentes, supondo α = 5 % :

Teste de Hipótese: H 0 : p h - p m = 0   ( ∆ 0 )   e       H 1 : p h - p m ≠ 0

Como na hipótese nula   ∆ 0 = 0 utilizamos a seguinte aproximação:

Z = p ^ h - p ^ m p ^ t 1 - p ^ t 1 n h + 1 n m ~ N 0,1

Onde:

p ^ t = 100 + 120 400 = 0,55

Passo 2

Vamos Construir nossa região critica: RC= z o ∈ R z 0 < - z α 2   o u   z 0 > z α 2

Onde:

z 0,025 = ± 1,96

Lembrando que o valor mostrado na tabela, é referente ao p = 0,5 - α 2 = 0,475 , quando o limite é bilateral.

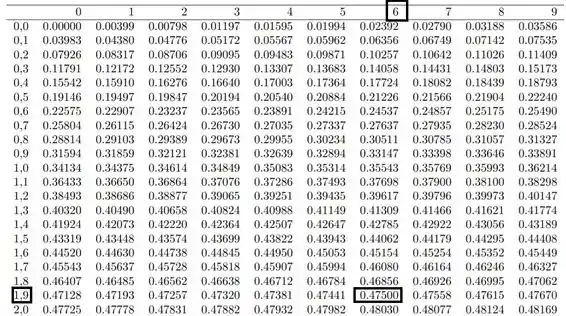
Portanto, a região critica assume a seguinte forma:

R C = z 0 < - 1,96   o u   z 0 > 1,96

Passo 3

Teste sob H 0 :

z 0 = 0,5 - 0,6 0,55   .   0,45   .   1 100 = - 2,01

Como z 0 = - 2,01 ∈ R C , rejeitamos H 0 e portanto existem evidencias de que o grau de fidelidade a um determiando produto é diferente entre os sexos.

Resposta

Construção do intervalo de confiança:

I C p h - p m ; 95 % = p ^ h - p ^ m ± z 0,025 . p ^ t 1 - p ^ t 1 n h + 1 n m =

= - 0,1 ± 0,0975 =

= - 0,1975   ;   - 0,0025

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quatro diferentes espécies de milho foram produzidas em laboratório. Deseja-se testar, a um nível de significância de α = 5 % , se existe diferença estatisticamente significativa entre as produtividad
Duas raças de cavalos estão sendo pesquisadas quanto à resistência a uma certa doença intestinal. O experimènto consiste em ministrar uma dieta especial, durante 3 meses e verificar a ocorrência ou nã
Estão sendo testados dois aparelhos para estabelecer suas respectivas confiabilidades no diagnóstico de uma certa doença. Dados foram obtidos de exames feitos em diversos pacientes, escolhidos ao acas
Queremos comparar três hospitais, através da satisfação demonstrada por pacientes quanto ao atendimento, durante o período de internação. Para tanto, foram selecionados, aleatoriamente, pacientes com
Para investigar os resultados do segundo turno de uma eleição estadual tomaram-se duasamostras de 600 eleitores cada: uma da capital e outra do interior. Da primeira, 276 disse-ram que votariam no can