Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 11.Exercícios propostos - Ex. 9
Testar se o nascimento de homens e mulheres é igualmente provável, se em uma pesquisa com 120 famílias de 4 crianças, escolhidas ao acaso, revelou ():
Passo 1
Olá galerinha, tudo bem com vocês? Primeiramente iremos relembrar a teoria.
Para este exercício iremos utilizar o Teste de aderência, onde admitimos, por hipótese, que a distribuição populacional seja descrita por determinado modelo de distribuição de probabilidade (tais como a Binomial, Normal, Poisson, etc.) e verificamos a boa ou má aderência dos dados amostrais ao modelo.
Iremos utilizar a seguinte equação, para sabermos se as diferenças existentes entre as frequências observadas e esperadas diferem significativamente:
Onde:
- estatística do teste, com graus de liberdade
- frequências observadas
- frequências esperadas
- número de elementos da amostra
- número de classes ou valores considerados
Então agora iremos seguir o roteiro:
- Enunciar as hipóteses, e .
- Fixar o nível de significância () do teste e escolher a variável , atentando para o número de graus de liberdade.
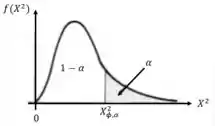
- Determinar a região crítica:
- Calcular a variável:
- Conclusão: se rejeita-se .
Passo 2
Então vamos lá para o nosso exercício:
- : nascimento é igualmente provável;
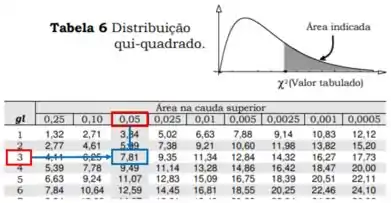
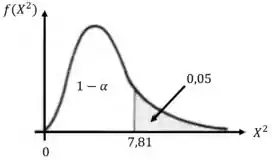
- Para determinarmos a região crítica iremos utilizar a Tabela de Distribuição qui-quadrado:
- Calcular a variável:
: nascimento não é igualmente provável.
Então:
Passo 3
- Sabemos que os eventos de uma distribuição binomial, obedecem a seguinte fórmula:
Onde:
No nosso exercício, temos 4 crianças, então:
Onde proporção de meninos.
Agora iremos determinar o valor de acordo com a distribuição de frequência observada ou real, a fim de determinarmos a probabilidade do nascimento de meninos:
De acordo com a frequência observada, o número médio de meninos é:
Igualando a média obtida à média teórica:
Portanto:
Sabemos que:
Porém, quando , podemos escrever:
Então:
Prontinho pessoal, até mais!
Resposta
, rejeita , ou seja, nascimento não é igualmente provável.