Em uma ANOVA de fator único com I tratamentos e J observações por tratamento, considere
- Expresse em função de
- Expresse
- Calcule
- Calcule
- Usando o resultado da parte , quanto vale E(QMTr) quando for verdadeiro? Quando for falso, quanto vale E(QMTr) comparado com ?
Passo 1
- O valor esperado de é
- O seguinte é verdadeiro
- O seguinte é verdadeiro
- O SSTr é dado por
- As hipóteses de interesse são
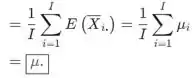
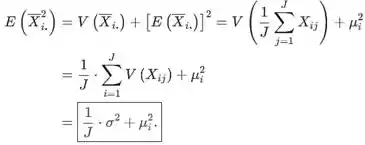
Passo 2
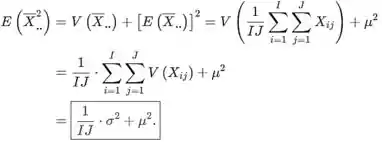
![]()
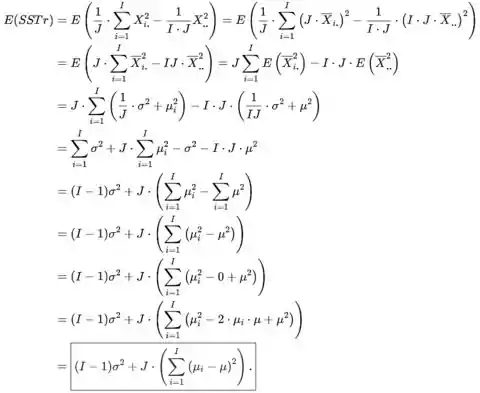
Passo 3
Usando isso e o fato de que
O valor esperado é
Versus a hipótese alternativa
Assumindo que é verdadeiro, então e por causa disso que
Substituindo isso, você obtém
Suponha que é verdade. Isso indica que existe i para o qual
E por conta disso
de onde podemos concluir que
Comparado com σ², os valores esperados são maiores.
Resposta
Ver o desenvolvimento.