Suponha que as observações de resistência de compressão sobre o quarto tipo de caixa no Exemplo 10.1 tenham sido 655,1, 748,7, 662.4, 679.0. 706,9 e 640,0 (obtidas adicionando-se 120 a cada anterior). Supondo que não haja nenhuma mudança nas observações restantes, efetue um teste F usando 0,05.
Passo 1
O resumo dos dados com o quarto tipo de mudança de caixa é
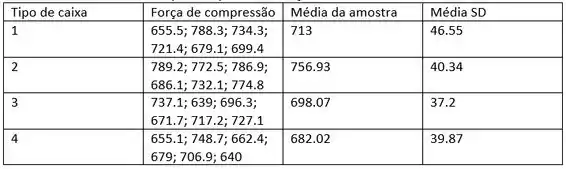
Os valores em negrito na tabela não são fornecidos, você deve calculá-los. Antes de calcular tudo o que é necessário para realizar o teste F, observe que existem
E
Passo 2
A tabela a seguir precisa ser preenchida com os valores correspondentes:

Assim, para o quarto tipo de caixa, a média amostral é
onde esta é a notação usada para a média amostral do iº tratamento (4º). O desvio padrão da amostra não é necessário. Os graus de liberdade são
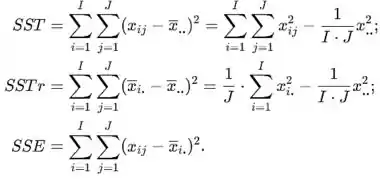
Os quadrados médios são
F é a razão dos dois quadrados médios
Calcule todos os valores um por um. Valor de
são dados (e calculados) e são
A partir disso, ou somando as linhas correspondentes, os valores de são
A grande média é
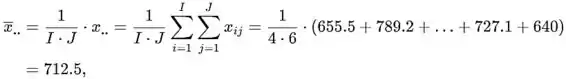
E
A soma total dos quadrados é
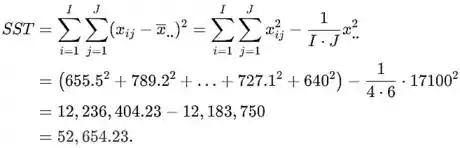
A soma dos quadrados do tratamento é
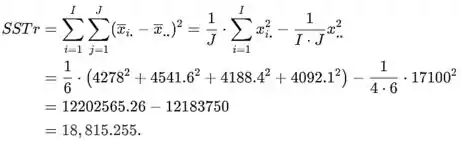
Identidade fundamental:
A soma dos quadrados do erro é
Passo 3
O valor da estatística F é

Quanto aos testes usuais, você pode tirar conclusões sobre as hipóteses observando o valor crítico de F ou um valor de P. Lembre-se que as hipóteses de interesse são
versus hipótese alternativa
O valor de P é a área à direita do valor de f sob a curva F onde F tem distribuição de Fisher com graus de liberdade 3 e 20; portanto
que foi calculado usando software (você pode estimá-lo usando a tabela no apêndice). Porque
rejeitar hipótese nula em determinado nível de significância. Há diferença nas forças de compressão entre as caixas.
Resposta
Rejeitar a hipótese nula