Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 10.Exercícios - Ex. 21

O artigo "The Effect of Enzyme Inducing Agents on the Survival Times of Rats Exposed to Lethal Levels of Nitrogen Dioxide" (Toxicology and Applied Pharmacology, 1978, p. 169-174) relata os seguintes dados sobre o tempo de sobrevivência de ratos que receberam dióxido de nitrogênio (70 ppm) por meio de diferentes dietas. Havia J 14 ratos em cada grupo.

a. Teste a hipótese nula, que postula que o tempo de sobrevivência médio real não depende da dieta, em relação à alternativa de que existe alguma dependência na dieta, usando 0,01. b. Suponha que 100(1 )% ICs para k funções paramétricas diferentes sejam calculados com base no mesmo conjunto de dados ANOVA. Então, verifica-se facilmente que o nível de confiança simultâneo é de pelo menos 100(1 k )%. Calcule os ICs com um nível de confiança simultâneo de pelo menos 98% para

Passo 1

  1. A hipótese de interesse são

    2. H 0   :   μ i =   μ j ,   i   ≠ j

    Versus a hipótese alternativa

    H a   : p e l o   m e n o s   d u a s   d a s   μ i   s ã o   d i f e r e n t e s

    onde é o verdadeiro tempo médio de sobrevivência do regime correspondente

    Note primeiro que

    I = 6 ,   t r a t a m e n t o s

    E

    J = 14 ,   a m o s t r a s   d e   c a d a   t i p o   -   r a t o s

    A tabela a seguir precisa ser preenchida com os valores correspondentes:

    Total de graus de liberdade

    I - 1 = 6 - 1 = 5 ;

    I J - 1 = 6 14 - 1 = 78 ;

    I J - 1 = 6 ∙ 14 - 1 = 83 .

    A soma total dos quadrados (SST), tratamento soma de quadrados (SSTr), e erro soma dos quadrados (SSE) são dados por

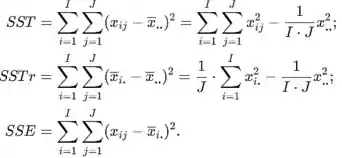
    Os quadrados médios são

    M S T r = 1 I - 1 S S T r ;

    M S E = 1 I J - 1 S S E

    F é a razão dos dois quadrados médios

    F = M S T r M S E

    Calcule todos os valores um por um. Valores de

    x - i = 1 J ∙ x i

    são dadas no exercício como

    x - 1 = 166 ;

    x - 2 = 303 ;

    x - 3 = 266 ;

    x - 4 = 212 ;

    x - 5 = 202 ;

    x - 6 = 184 ;

    A grande média x - . . é

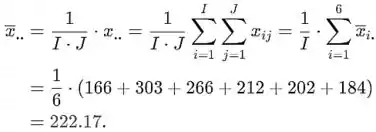
    A soma dos quadrados do tratamento é

    Passo 2

    A soma dos quadrados dos erros é

    A identidade fundamental:

    S S T = S S T r + S S E

    S S T = S S T r + S S E = 19006 + 131183 = 321259

    Os quadrados médios podem ser calculados agora como

    M S T r = 1 I - 1 S S T r = 1 5 190076 = 38015.1 ;

    M S E = 1 I J - 1 S S E = 1 6 14 - 1 131183 = 1681.83  

    O valor estatístico de F é

    f = M S T r M S E = 380115.1 1681.83 = 22.6

    A tabela ANOVA agora se torna

    Quanto aos testes usuais, você pode tirar conclusões sobre as hipóteses observando o valor crítico de F ou um valor de P. Lembre-se que as hipóteses de interesse são

    H 0   :   μ i = μ j ,   i   ≠ j

    Versus a hipótese alternativa

    H a   : p e l o   m e n o s   u m a   d a s   μ i   é   d i f e r e n t e

    O valor de P é a área à direita do valor de f sob a curva F onde F tem distribuição de Fisher com graus de liberdade 5 e 78; portanto

    P = P F > f = P F > 22.6 ≈ 0

    que foi calculado usando software (você pode estimá-lo usando a tabela no apêndice). Porque

    P = 0 < 0.01 = α

    Rejeitar a hipótese nula em determinado nível de significância. Há diferença estatisticamente significativa nas médias verdadeiras entre os seis tempos de sobrevida diferentes.

    Usando a tabela, você pode usar, por exemplo, valor F 0,01,5 , 60 (isto é aproximado) para o qual a área sob a curva FF à direita de F 0,01,5 , 60 é 0,01. O valor é

    F 0.01,5 , 60 = 4.6 < 22.6 = f

    o que indica rejeitar a hipótese nula no nível de significância 0.01

    Passo 3

  2. Primeiro intervalo:

M S E = 1681.83

Usando o fato de que a variável aleatória

θ =   X - 1 - 1 5 X - 2 + X - 3 + X - 4 + X - 5 + X - 6

tem aproximadamente distribuição de estudantes com I ( J - 1 ) = 78 graus de liberdade, pelo fato

P t α 2,78 <   X - 1 - 1 5 X - 2 + X - 3 + X - 4 + X - 5 + X - 6 < t α 2,87 = 1 - α

onde, neste caso, α = 0.02 , e da tabela no apêndice é aproximadamente

t α ,   2,8 = t 0.01,78 = 2.645

o intervalo de confiança de 98 % (consulte a página 424) é

∑ i = 1 6 c i x - i ± t α 2 , I J - I M S E ∑ i = 1 6 c i 2 J

Aqui MSEMSE é estimativa de variância σ ²

Desde c 1 = 1 e c i =   - 1 5 ,   i = 2,6 , … , 6

∑ i = 1 6 c i 2 = 1.2

Estimando θ

θ =   X - 1 - 1 5 X - 2 + X - 3 + X - 4 + X - 5 + X - 6 = - 67.4

onde todos os valores são dados na tabela do exercício. Portanto, o intervalo de confiança de 98 % para θ é

- 67.4 ± 2.645 1681.83 ∙ 1.2 14  

Ou igualmente

- 99.16 , - 35.64

Segundo intervalo:

M S E = 1681.83

Usando o fato de que a variável aleatória

θ =   0 ∙ X - 1 + 1 4 X - 2 + X - 3 + X - 4 + X - 5 - X - 6

tem aproximadamente distribuição de estudantes com I ( J - 1 ) = 78 graus de liberdade, pelo fato

P t α 2,78 <   θ =   0 ∙ X - 1 + 1 4 X - 2 + X - 3 + X - 4 + X - 5 - X - 6 = 1 - α

onde, neste caso, α = 0.02 , e da tabela no apêndice é aproximadamente

t α ,   2,8 = t 0.01,78 = 2.645

o intervalo de confiança de 98 % (consulte a página 424) é

∑ i = 1 6 c i x - i ± t α 2 , I J - I M S E ∑ i = 1 6 c i 2 J

Aqui MSEMSE é estimativa de variância σ ²

Desde c 1 = 1 e c i =   - 1 5 ,   i = 2,6 , … , 6

∑ i = 1 6 c i 2 = 1.2

Estimando θ

θ ^ = 61.75

onde todos os valores são dados na tabela do exercício. Portanto, o intervalo de confiança de 98 % para θ é

61.75 ± 2.645 1681.83 ∙ 1.25 14  

Ou igualmente

29.34,94.16

Resposta

  1. Rejeitar a hipótese nula
  2. - 99.16 , - 35.64 ;   29.34,94.16

Exercícios de Livros Relacionados

Suponha que Xij seja uma variável binominal com parâmetros n e pi (portanto, aproximadamente normal quando npi 5 e nqi 5). Então, visto que i npi , V(Xij) 2 i npi (1 pi ) i (1 i /n), como os Xijs deve
Amostras de seis diferentes marcas de imitação da margarina diet foram analisadas para determinar o nível de ácidos graxos poli-insaturados fisiologicamente ativos (AGPFA, em porcentagem), gerando os
Use o procedimento de Tukey nos dados do Exercício 6 para identificar diferenças no tempo de vôo médio real entre os quatro tipos de mosquito.
A tabela ANOVA parcial apresentada a seguir é reproduzida do artigo "Perception of Spatial Incongruity" (J. Nervous and Mental Disease, 1961 p. 222), no qual a capacidade de cada um dos três diferente
Em um experimento para comparar a resistência à tração de I = 5 em tipos diferentes de fio de cobre foram usadas J = 4 amostras de cada tipo. As estimativas entre as amostras e dentro das amostras de