Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 10.Exercícios - Ex. 22
Os dados a seguir referem-se à produção de tomates (kg/lote) para quatro níveis diferentes de salinidade; aqui, o nível de salinidade refere-se à condutividade elétrica (CE), onde os níveis escolhidos foram CE 1,6; 3,8; 6,0 e 10,2 nmhos/cm:
Use o teste F no nível 0,05 para testar quaisquer diferenças na produção média real provocadas por níveis de salinidade diferentes
Passo 1
A hipótese de interesse são
Versus a hipótese alternativa
onde estão o verdadeiro rendimento médio devido aos diferentes níveis de salinidade.
Os tamanhos das amostras dos tratamentos são desiguais; assim, a ANOVA para tamanhos de amostra desiguais deve ser usada. A tabela a seguir resume as quantidades.
O seguinte é necessário para entender como calcular as quantidades mencionadas e necessárias.
Tamanhos de amostra desiguais
Seja sejam os tamanhos de amostra dos tratamentos I e sejam ser o número total de observações. Denote com
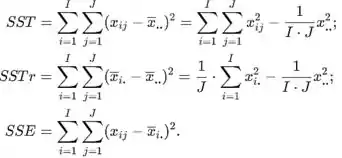
com graus de liberdade, respectivamente,
Os quadrados médios são
F é a razão dos dois quadrados médios
O valor P é a área sob o curva à direita de f. Calcular tudo um por um. Começando com a soma das observações no iº tratamento
e as médias do iº tratamento são
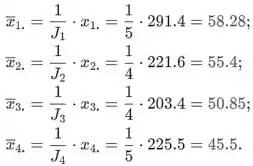
Passo 2
A grande soma é
A grande média é
Os graus de liberdade são, para
A soma total dos quadrados é
A soma dos quadrados do tratamento é
Da identidade fundamental
Os quadrados médios são
F é a razão dos dois quadrados médios
Passo 3
O valor P é a área sob o curva para a direita de f
que foi computado por meio de um software; você pode estimar o valor usando a tabela no apêndice como
onde a área à direita de sob o curva é 0.05, e porque
Rejeitar a hipótese nula em determinado nível significativo. Além disso, se você usou o valor P, porque
rejeitar hipótese nula em determinado nível significativo. A conclusão é que existe uma diferença significativa no rendimento de tomates para os diferentes níveis de salinidade.
Resposta
rejeitar hipótese nula