Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 10.Exercícios - Ex. 32
Em um experimento para comparar a qualidade de quatro diferentes marcas de fitas de gravação magnética, foram selecionados cinco carretéis de 2400 pés de cada marca (A-D), determinando-se em seguida o número de defeitos.
Acredita-se que o número de defeitos tenha, aproximadamente, uma distribuição Poisson para cada marca. Analise os dados ao nível de significância 0,01 para verificar se o número esperado de defeitos por carretel é o mesmo para cada marca
Passo 1
Os dados fornecidos, devem ser transformados usando
porque os dados seguem a distribuição de Poisson para cada marca.
As hipóteses de interesse são
Versus a hipótese alternativa
Onde é é a verdadeira média da marca
O dado transformado é dado na tabela abaixo
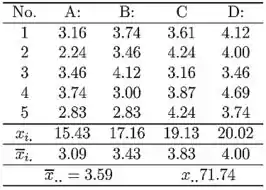
Esta tabela resume tudo o que é necessário para realizar o teste F (ANOVA). Aqui está a explicação de como obter esses valores.
Observe primeiro que
E
A tabela a seguir precisa ser preenchida com os valores correspondentes:
Os graus de liberdade são
Denotado que
A soma total dos quadrados (SST), tratamento soma de quadrados (SSTr), e erro soma dos quadrados (SSE) são dados por
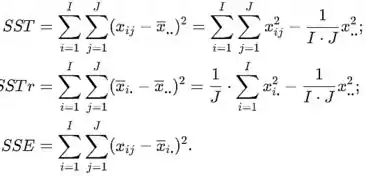
Os quadrados médios são
F é a razão dos dois quadrados médios
Calcule todos os valores um por um. Ao somar as colunas correspondentes (geralmente linhas), valores de são
Os valores
São dados por
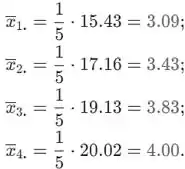
Passo 2
A grande média é
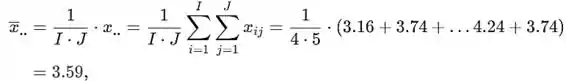
E
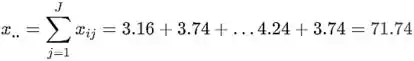
A soma total dos quadrados é
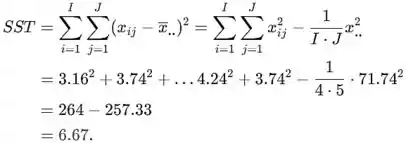
A soma dos quadrados do tratamento é
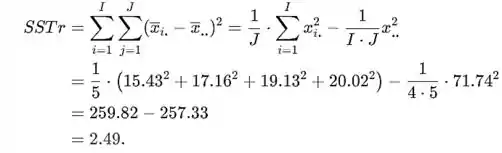
Passo 3
A identidade fundamental:
A soma dos quadrados do erro é
Os quadrados médios podem ser calculados agora como
O valor da estatística F é
A tabela ANOVA agora se torna
Quanto aos testes usuais, você pode tirar conclusões sobre as hipóteses observando o valor crítico de F ou um valor de P. Lembre-se que as hipóteses de interesse são
Versus a hipótese alternativa
O valor P é a área à direita do valor f sob a curva F onde F tem distribuição de Fisher com graus de liberdade 3 e 16; portanto
que foi calculado usando software (você pode estimá-lo usando a tabela no apêndice). Porque
não rejeite a hipótese nula em determinado nível de significância. Não há diferença estatisticamente significativa nas médias verdadeiras entre os quatro tipos diferentes de marcas.
Usando a tabela, você pode usar, por exemplo, valor para o qual a área sob a curva FF à direita de é 0.01. O valor é
o que indica não rejeitar a hipótese nula ao nível de significância 0,01.
Resposta
Não rejeitar a hipótese nula