Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 15.Exercícios - Ex. 34
Um artigo em Quality Engineering (1999-2000) Experimentos fatoriais em estudos de plantas-piloto. Reporta um experimento de investigação do efeito de temperatura (A), da produção de gás (B) e da concentração (C) sobre a a resistência da solução de um produto em uma unidade de recirculação. Dois blocos foram usados com ABC superpostos, sendo o experimento replicado duas vezes. Os dados são apresentados a seguir.
- Analise os dados desse experimento.
- Analise os resíduos e comente a adequação do modelo.
- Comente a eficiência desse planejamento. Note que replicamos o experimento duas vezes, mas não temos informação sobre a interação ABC.
- Sugira um planejamento melhor, espeficique um que forneça alguma informação sobre todas as interações.
Passo 1
Opa, tranquilo galera? Espero que sim! Se não, bora resolver essa questão de estatística e ficar suave! Então, assumindo uma distribuição normal para o item a):
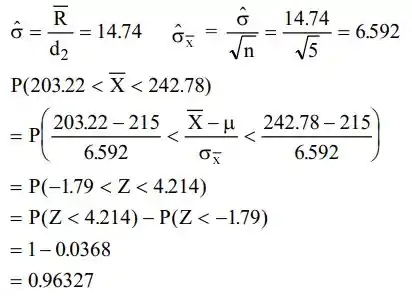
Probabilidade de 96% para essa questão.
Passo 2
Para o problema superposto segue o sistema para a probabilidade mais correta possível. Com probabilidade próxima de 96% a gente consegue perceber que existe uma probabilidade alta de certa forma para os tipos dados.