Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 8.Exercícios - Ex. 80
Um artigo na revista Journal of sports science apresenta resultados de uma investigação do nível de hemoglobina dos jogadores de hóquei no gelo nas olimpíadas do Canadá. Os dados recortados em (g/dl) são mostrados a seguir:
- fornecido seguinte gráfico de probabilidade dos dados, qual é a sua posição lógica acerca da distribuição básica dos dados?
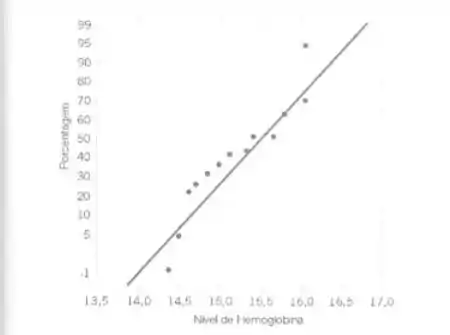
- Explique porque essa verificação da distribuição baseando-se nos dados amostrais será importante se quisermos construir o intervalo de confiança para a média.
- Baseando-se nesses dados amostras, o intervalo de confiança de 95% para a média é [15.04; 15.62]. É razoável inferir que a média verdadeira poderia ser 14.5? Explique sua resposta.
- Explique porque essa verificação da distribuição baseando-se nos dados amostrais será importante se quisermos construir o intervalo de confiança para variância.
- Baseando-se nesses dados amostrais, no intervalo de confiança de 95% para variância é [0.22; 0.82]. É razoável inferir que a variância verdadeira poderia 0.35? Explique sua resposta.
- É razoável usar esse intervalo de confiança para inferir sobre a média e a variância dos níveis de hemoglobina
(i) de doutores canadenses? Explique sua resposta.
(ii) De criança de canadenses de seis a 12 anos? Explique sua resposta.
Passo 1
Letra a:
A distribuição subjacente dos dados é aproximadamente normal, porque não há curvatura forte no gráfico de probabilidade normal e o padrão parece ser aproximadamente linear.
Passo 2
Letra b:
A verificação é importante, porque se a distribuição subjacente dos dados não é aproximadamente normal (e se a amostra não for muito grande), então o intervalo de confiança pode ser impreciso.
Passo 3
Letra c:
Não, não é razoável que a verdadeira média possa ser 14.5, porque o intervalo de confiança para a média não contém 14.5 e, portanto, uma média de 14.5 é improvável de ocorrer.
Passo 4
Letra d:
A verificação é importante, porque se a distribuição subjacente dos dados não são aproximadamente normais, então o intervalo de confiança pode ser impreciso.
Passo 5
Letra e:
Sim, é razoável inferir que a verdadeira variância poderia ser 0.35, porque o intervalo de confiança para a variância contém o valor de 0.35.
Passo 6
Letra f:
A amostra contém dados dos jogadores olímpicos canadenses de hóquei no gelo. Então, não é razoável fazer uma inferência sobre a média e a variância dos níveis de hemoglobina de médicos canadenses nem de crianças canadenses, porque seus níveis de hemoglobina podem ser muito diferentes dos níveis de hemoglobina de os jogadores olímpicos canadenses de hóquei no gelo.
Resposta
- A distribuição subjacente dos dados é aproximadamente normal.
- Se a distribuição subjacente dos dados não for aproximadamente normal (e se a amostra não for muito grande), então o intervalo de confiança pode ser impreciso.
- Não
- A distribuição subjacente dos dados não é aproximadamente normal, então o intervalo de confiança pode ser impreciso.
- Sim
- Não e não