Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 14.Exercícios - Ex. 64
Um artigo em Tropical Science (Proximate Composition of the Seeds of Acacia Nilotica var Adansonti (Bagaruwa) e Extração de Sua Proteína, 1992, Vol. 32, N.° 3, pp. 263-268) reportou uma pesquisa sobre estração e concentração de proteínas das sementes de acácia para alimentação na pecuária da Nigéria, de modo a eliminar as substâncias tóxicas das sementes. A tabela a seguir mostra os efeitos do tempo de extração e a razão entre a farinha e o solvente sobre a capacidade de extração de proteína das sementes de bararuwa em água destilada:
Todos os valores represental médias de três determinações.
Teste as hipóteses apropriadas e tire conclusões usando a análise de variância com .
Analise graficamente a interação.
Analise os resíduos desse experimento.
Passo 1
Bom galera, nós testar se há efeito de algum dos dois fatores. Para isso, as hipóteses a serem testadas são:
todo ou pelo menos um ,
todo ou pelo menos um ,
todo ou pelo menos um
Passo 2
Belezinha, agora considerados os dois fatores e . indica o total de observações realizadas no nível do fator , indica o total de observações feitas no nível do fator , Indica o total de observações nas células , e indica a quatidade total de observações. Definindo , , e correspondem a células, colunas, células e média geral. Usamos para a analise de variância as formulas:
Passo 3
Show de bola, para testar se os efeitos do fator de linha são todos iguais a zero (), usamos a razão , que tem uma distribuição com e graus de liberdade.
Para testarmos se os efeitos do fator de coluna são todos iguais a zero (), usamos a razão , que tem uma distribuição com e graus de liberdade.
Para testarmos se todos os efeitos de interação são zero, usamos a razão , que uma distribuição com e graus de liberdade.
Geralmente é melhor realizar o teste para a interação antes e depois avaliar os principais efeitos. Se a interação não for significativa, a interpretação do teste sobre os principais efeitos é simples. Se a interação for significativa, os principais efeitos envolvidos na interação podem não ter muito valor interpretativo prático.
Passo 4
Então agora fazemos a analise de variância no Minitab, e temos como resultado:
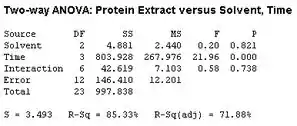
Como o valor do teste para interação é de , que é superior a , concluímos que no nível a interação não é significativa. Portanto, podemos continuar testando a hipótese para os principais efeitos.
Uma vez que os valores dos testes para os efeitos da linha e coluna são e , no nível rejeitamos apenas a hipótese nula para o fator Tempo e concluímos que há efeito do tempo e não evidencia do efeito do solvente.
Passo 5
Vamos então traçar o gráfico de interação para pelo Tempo em diferentes níveis de Solvente. O Gráfico fica:
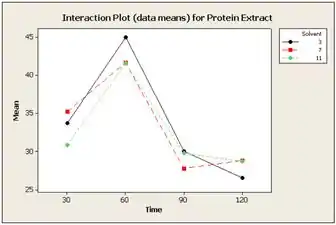
Embora os segmentos de linha se cruzem, eles são quase paralelos. Portanto, não devemos esperar um interação significativa no experimento.
Passo 6
Por fim, vamos fazer a analise de resíduos, para isso construiremos o gráfico de probabilidade normal, o de resíduos por valores, e os de resíduos por tempo e resíduos por solvente, obetermos:
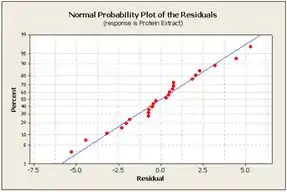
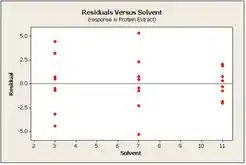
Com isso concluímos que o gráfico de probabilidade normal não indica qualquer discrepância da normalidade. Os lotes de resíduos são bastantes simétricos sobre zero. Portanto, nós concluímos que o modelo é adequado.
Resposta
Há efeito do tempo e não evidencia do efeito do solvente.
Não devemos esperar um interação significativa no experimento.
Concluisse que o modelo é adequado.