Considere um fatorial sem réplicas e suponha que uma das combinações de tratamentos esteja faltado. Uma abordagem lógida a esse problema é estimar o valor que falta com um número que torne zero a estimativa da mais alta ordem de interação. Aplique essa técnica aos dados no Exemplo , suponto que esteja faltando. Compare os resultados das analises desses dados com os resultados do Exemplo .
Passo 1
Bom galera, para o experimento fatorial temos a tabela:
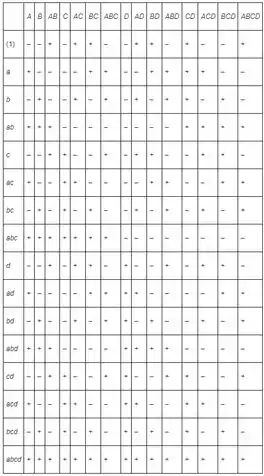
Passo 2
Belezinha, agora estimando o efeito de a forma como o efeito da maior interação,
Encontramos agora todos os efeitos de todos os fatores com o novo valor de . Usamos a tabela de sinais correspondentes na coluna do fator considerado. A tabela dos efeitos para todos os fatores e interações é:

Passo 3
Show de bola, agora para encontrarmos os efeitos significantes devemos plotar um gráfico de probabilidade normal dos efeitos, fica assim:
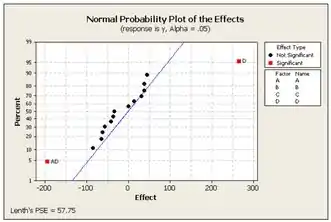
O mostra que os fatores e são significantes, enquanto que o antigo valor para foram significativos para , e
Resposta
O mostra que os fatores e são significantes, enquanto que o antigo valor para foram significativos para , e