Enunciado

Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 2.4 - Ex. 39

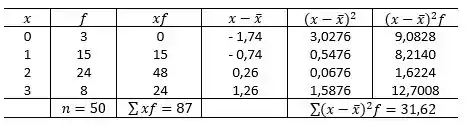
Cálculos usando dados agrupados. Construa uma distribuição de frequência para os dados. A seguir, use a tabela para estimar a média e o desvio padrão amostral do conjunto de dados.

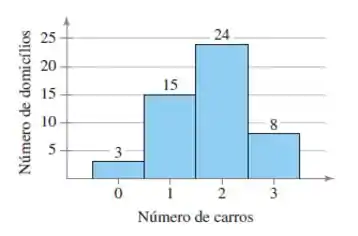
Carros por domicílio. Os resultados de uma amostra aleatória do número de carros por domicílio em certa região são mostrados no histograma.

Passo 1

Olá pessoal, vamos fazer esse exercício juntos?

Primeiramente, vamos relembrar a equação da média e do desvio padrão amostral de dados agrupados:

Pela figura do enunciado, temos:

número de carros
número de domicílios

Passo 2

Agora vamos montar nossa tabela, com os valores de e :

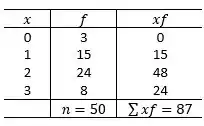
Com isso, conseguimos calcular a média amostral:

Passo 3

Com o valor da média, iremos montar a segunda parte da tabela, para o cálculo do desvio padrão amostral:

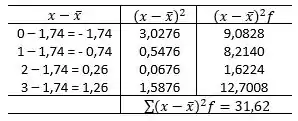
Por fim, calculamos o desvio padrão:

Foi fácil esse né galerinha? Então, vamos fazer mais um exercício juntos?

Resposta

Exercícios de Livros Relacionados

Para verificar a homogeneidade das duas populações do problema anterior, um estatístico sugeriu que se usasse o quociente F = v a r ( X / A ) v a r ( X / B ) , mas não disse qual decisão tomar baseado

Para se estudar o desempenho de duas corretoras de ações, selecionou-se de cada uma delas amostras aleatórias das ações negociadas. Para cada ação selecionada, computou-se a porcentagem de lucro apres

Como vimos na seção 3.3 , o desvio padrão é bastante afetado pela magnitude dos dados, ou seja, ele não é uma medida resistente. Se quisermos comparar a variabilidade de dois conjuntos de dados podemo

Calcule o desvio absoluto mediano para as populações do CD-Brasil.

Considere a situação do Exercício 1.28, mas agora use o seguinte conjunto de dados, no qual o encolhimento é medido novamente em velocidades de injeção baixa e alta. Entretanto, dessa vez a temperatur