Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 9.Problemas - Ex. 38
Uma certa região florestal foi dividida em 109 quadrados para estudar a distribuição de Primula Simenses Selvagem. A priori, supomos que esse tipo distribua-se aleatoriamente na região. O quadro abaixo indica o número de quadrados com X Primula Simenses; o número médio de plantas por quadrado foi de 2,2.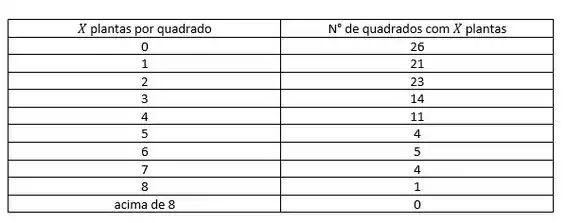
(a) Se as plantas realmente se distribuem aleatoriamente na região, qual a probabilidade de encontrarmos pelo menos duas Primulas?
(b) Dê as freqüências esperadas para os valores de X = 0, X = 1 e X = 2.
(c) Apenas comparando os resultados de (b) com as freqüências observadas, qual a conclusão a que você chegaria?
(d) Quais as causas que você daria para a conclusão?
Passo 1
(a) Supondo que , tem-se:
Passo 2
(b) A tabela a seguir traz o as frequências esperadas para X=0, X=1 e X=2, calculadas por .
Passo 3
(c) A observação dos resultados anteriores, indica que as plantas não se distribuem de acordo com a distribuição de Poisson com parâmetro 2,2.
Passo 4
Dependência , pois a reprodução na vizinhança é mais provável do que longe.
Resposta
Ei, a resposta está no passo a passo :)