Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 4.3 - Ex. 4
Num certo bairro da cidade de São Paulo, as companhias de seguro estabeleceram o seguinte modelo para o número de veículos furtados por semana:
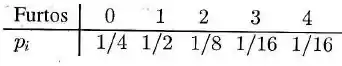
calcule a média e a variância do número de furtos semanais desse bairro.
Passo 1
Eaí, tudo bem? Bora resolver esse exercício?
O exercício pede para calcular média e a variância do número de furtos semanais desse bairro.
Você se lembra das fórmulas? Se não, bora dar aquela revisão!
Então, estamos esperando o quê?
Passo 2
Primeiramente, vamos calcular a média, já que a fórmula da variância depende desse valor. Assim, temos que:
Assim,
Passo 3
Agora, substituindo esse valor na fórmula da variância, temos que:
Ou seja,
Resposta
Logo, concluímos que e que
Exercícios de Livros Relacionados
Suponha que a variável de interesse tenha a distribuição como na figura abaixo.Você acha que a média é uma boa medida de posição? E a mediana? Justifique.
As taxas de juros recebidas por 10 ações durante um certo período foram (medidas em porcentagem) 2,59 ; 2,64 ; 2,60 ; 2,62 ; 2,57 ; 2,55 ; 2,61 ; 2,50 ; 2,63 ; 2,64 . Calcule a média, a mediana e o de
Para facilitar um projeto de ampliação da rede de esgoto de uma certa região de uma cidade, as autoridades tomaram uma amostra de tamanho 50 dos 270 quarteirões que compõem a região, e foram encontrad
Um rebite é montado num furo; o diâmetro médio dos rebites fabricados vale 12m m e seu desvio padrão 0,2m m ; o diâmetro médio dos furos produzidos vale 13m m e seu desvio padrão 0,5m m . Chamando de
De fitas metálicas, cuja largura média vale 300m m e desvio padrão 3m m , são retiradas as rebarbas laterais, de largura constante e igual a 10m m cada uma, e depois são cortadas: 12 tiras do tipo A,