Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 15.Exercícios - Ex. 36

Considere os dados do exercício 10 - 36 . Use o teste dos sinais, com α = 0,05 . Para determinar se a diferença Mas leituras da mediana na impureza entre os dois testes analíticos.

Passo 1

Bom galera, Os parâmetros de interesse são medianas da população são de medições representadas pelas duas amostras.

Devemos testar se as medianas da população são de medições representadas pelas duas amostras são diferentes ou não.

Para esse objetivo, temos a hipótese nula:

H 0 : Não há diferença nas medianas de ambas populações

H 0 : μ ~ 1 = μ ~ 2   e q u i v a l e n t e   á   H 0 : μ ~ D = 0

H 1 : Há diferença nas medianas de ambas as populações

H 0 : μ ~ 1 ≠ μ ~ 2   e q u i v a l e n t e   á   H 0 : μ ~ D ≠ 0

Com a significância α = 0,05 .

Passo 2

Usaremos os valores de tabela do teste de sinal para realizar este teste.

Então a estatísticas de teste é r = m i n ⁡ ( r + , r - )

Uma vez que α = 0,05 e n = 8 , o valor critico r 0,05 = 0 . Nós podemos rejeitar H 0 em favor de H 1 se r ≤ 0 .

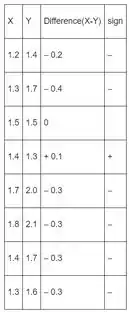
A parte da tabela, notamos que r + = 1 , r - = 6 , e assim r = min ⁡ 1,6 = 1

Uma vez r = 1 , não rejeitamos a hipótese nula de que as medianas da população são de medições representadas pelas duas amostras são as mesmas.

Assim, podemos concluir que as medianas da população de medições apresentadas pelos duas amostras são as mesmas.

Resposta

As medianas da população de medições apresentadas pelos duas amostras são as mesmas.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O fabricante de uma banheira está interessado em testar dois aquecedores diferentes para seu produto. O aquecedor que produzir o máximo calor ganho depois de 15 minutos será o preferível. Ele obtém 10
Uma engenheira eletricista tem de projetar um circuito para operar com uma quantidade máxima de corrente em um tubo de imagem, de modo a encontrar uma imagem com brilho suficiente. Dentro de suas rest
Considere os dados de taxa de ataque químico do exercício 10-17.a)Use o teste de Wilcoxon da soma dos postos para investigar a afirma;’ao de que a taxa média de ataque químico é a mesma para ambas as
Considere a distancia viajada por uma bola de golfe descrita no exercício 10-27.a)Use o teste de Wilcoxon da soma dos postos para investigar se as medias diferem. Use α = 0.05 .b)Use a aproximação nor
Considere os dados da primeira réplica do Exercício 14-13.a)Construa um planejamento com dois blocos de oito observações cada, com ABCD superposto.b)Analise os dados.