Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 16.Exercícios - Ex. 38
Um gráfico X usa amostras de tamanho 4. A linha central está em 100 e os limites 3-sigma, superior e inferior de controle estão em 106 e 94, respectivamente.
a)Qual é a do processo?
b)Suponha que a média do processo se desloque para 96. Encontre a probabilidade de essa mudança ser detectada na próxima amostra.
c)Encontre o CMC para detectar a mudança no item (b).
Passo 1
Hey, jovem, tudo bem contigo? Espero que sim 😊 Bora pra mais uma questãozinha de estatística? Vamo que vamo! Então, (a) para o processo temos um sigma padrão aproximado de:
(b)Para essa probabilidade temos uma chance de:
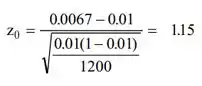
(c)CMC aproximado de 11.5% para razão de 1.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Um experimento para investigar o tempo de sobrevivência, em horas, de um componente eletrônico, consiste em colocar as partes em uma célula de teste e corrê-las durante 100 horas sob condições de temp
Considere a amostra x 1 ,x 2 ,. . . ,x n , com média da amostra e desvio padrão da amostra s. Seja z i = ( x i - x _ ) / s ,i = 1,2 , . . . ,n . Quais são os valores da média e dos desvio padrão da am
Usando os resultados do Exercício 6-96, qual das duas quantidade ∑ i = 1 n ( x i - x _ ) 2 e ∑ i = 1 n ( x i - μ ) 2 será menor, de modo que x _ ≠ μ ?
Considere a quantidade ∑ i = 1 n ( x i - a ) 2 . Para que valor de a essa quantidade é minimizada?]
Considere os dados do aerofólio do exercício seis. 12. Subtraia 30 de cada valor então multiplique as quantidades resultantes por 10. Agora calcule s para os novos dados. Como essa grandeza está relac