Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Meyer - Aplicações a Estatística- Ed: 2º - Capítulo 1.Problemas - Ex. 8

Considere quatro objetos, a ,   b ,   c ,   d . Suponha que a ordem em que tais objetos sejam listados represente o resultado do experimento. Sejam os eventos e definidos assim: A = a   e s t á   n a   p r i m e i r a   p o s i ç ã o e B = b   e s t á   n a   s e g u n d a   p o s i ç ã o .

  1. Enumere todos os elementos do espaço amostral.
  2. Enumere todos os elementos dos eventos A ⋂ B   e A ⋃ B .

Passo 1

Fala aí, galerinha do Responde aí. Simbora aprender estatística?

Primeiramente, na letra a, devemos determinar todo o espaço amostral. Isto é, o conjunto de todas as possibilidades de retirada. Fazendo um diagrama esquemático:

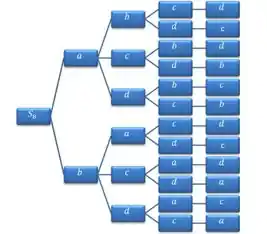
Portanto, o espaço amostral é:

S = { a b c d ,   a b d c ,   a c b d ,   a c d b ,   a d b c ,   a d c b ,   b a c d ,   b a d c ,   b c a d ,   b c d a ,   b d a c ,   b d c a ,   c a b d ,   c b a d …

… c b d a ,   c d a b ,   c d b a ,   d a b c ,   d a c b ,   d b a c ,   d b c a ,   d c a b ,   d c b a }

Passo 2

Para a letra b, precisamos determinar os conjuntos. Sabemos que:

A = a b c d ,   a b d c ,   a c b d ,   a c d b ,   a d b c ,   a d c b

B = ( a b c d ,   a b d c ,   c b a d ,   c b d a ,   d b a c ,   d b c a }

Portanto, a interseção será:

A ⋂ B = a b c d , a b d c

Já a união, será:

A ⋃ B = { a b c d ,   a b d c ,   a c b d ,   a c d b ,   c b a d ,   c b d a ,   d b a c ,   d b c a }

Resposta

  1. S = { a b c d ,   a b d c ,   a c b d ,   a c d b ,   a d b c ,   a d c b ,   b a c d ,   b a d c ,   b c a d ,   b c d a ,   b d a c ,   b d c a ,   c a b d ,   c b a d …

    … c b d a ,   c d a b ,   c d b a ,   d a b c ,   d a c b ,   d b a c ,   d b c a ,   d c a b ,   d c b a }

A ⋂ B = a b c d , a b d c ;   A ⋃ B = { a b c d ,   a b d c ,   a c b d ,   a c d b ,   c b a d ,   c b d a ,   d b a c ,   d b c a }

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma urna contém duas bolas brancas (B) e três bolas vermelhas (V). Retira-se uma bola ao acaso da urna. Se for branca, lança-se uma moeda; se for vermelha, ela é devolvida à urna e retira-se outra. Dê
(c) Investigam-se famílias com três crianças, anotando-se a configuração segundo o sexo.
(f) Um fichário com dez nomes contém três nomes de mulheres. Seleciona-se ficha após ficha, até o último nome de mulher ser selecionado, e anota-se o número de fichas selecionadas.
(j) De um grupo de cinco pessoas {A, B, C, D, E}, sorteiam-se duas, uma após outra, com reposição, e anota-se a configuração formada.
Duas moedas são lançadas. Dê dois possíveis espaços amostrais para esse experimento. Represente um deles como o produto cartesiano de dois outros espaços amostrais (ver Morettin et al., 1999, para o c