Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 4.Exercícios - Ex. 87

87. Construa um gráfico de probabilidade que permita avaliar a normalidade da distribuição lognormal como um modelo para os dados de precipitação do Exercício 81 (Capítulo 1).

Passo 1

Fala galerinha boa! Tudo bem com vocês? Vamos fazer mais um exercício.

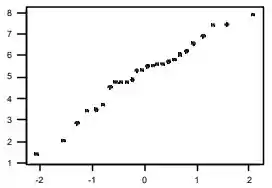
Para verificar a plausibilidade de uma distribuição lognormal populacional para os dados de chuva do Exercício 81 no Capítulo 1, pegue os logs naturais e construa um gráfico de probabilidade normal. Este gráfico e um gráfico de probabilidade normal para os dados originais. Claramente, a transformação logarítmica dá um gráfico bastante direto, então a lognormalidade é plausível. A curvatura no gráfico para os dados originais implica uma distribuição populacional positivamente assimétrica - como a distribuição lognormal.

Até a próxima, pessoal!

Resposta

No passo 1.

Exercícios de Livros Relacionados

81. O gráfico de probabilidade normal a seguir foi construído a partir de uma amostra de 30 leituras de tensão na malha de pontos de tubos de vídeo usados em monitores de computadores. Parece plausíve

84. O artigo “A Probabilistic Model of Fracture in Concrete and Size Effects on Fracture Toughness” (Magazine of Concrete Res., 1996, p. 311-320) fornece argumentos que explicam por que a distribuição

86. O artigo “The Load-Life Relationship for M50 Bearings with Silicon Nitride Ceramic Balls” (Lubrication Engr., 1984, p. 153-159) relata os dados a seguir sobre a vida de carga de mancais (milhões r

88. As observações a seguir são valores de precipitação no mês de março de um período de 30 anos em Minneapolis-St. Paul.0,77 1,20 3,00 1,62 2,81 2,48 1,74 0,47 3,09 1,31 1,87 0,96 0,81 1,43 1,51 0,32

89. Use um software estatístico para construir um gráfico de probabilidade normal dos dados do limite de resistência à tração fornecidos no Exercício 13 do Capítulo 1 e comente.