Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 4.Exercícios - Ex. 86
86. O artigo “The Load-Life Relationship for M50 Bearings with Silicon Nitride Ceramic Balls” (Lubrication Engr., 1984, p. 153-159) relata os dados a seguir sobre a vida de carga de mancais (milhões revs.) para mancais testados com cargas de 6,45 kN.
47,1 68,1 68,1 90,8 103,6 106,0 115,0 126,0 146,6 229,0 240,0 240,0 278,0 278,0 289,0 289,0 367,0 385,9 392,0 505,0
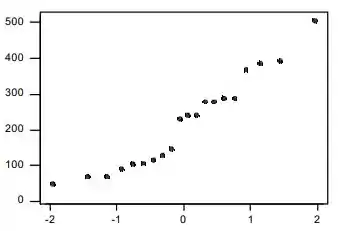
a. Construa um gráfico de probabilidade normal. A normalidade é plausível?
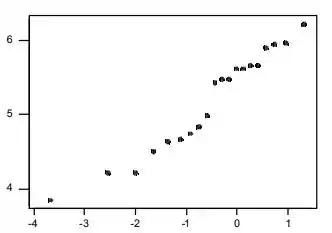
b. Construa um gráfico de probabilidade de Weibull. A família de distribuições Weibull é plausível?
Passo 1
Fala galerinha boa! Tudo bem com vocês? Vamos fazer mais um exercício.
a) Os 10 maiores percentis z são 1,96, 1,44, 1,15, 0,93, 0,76, 0,60, 0,45, 0,32, 0,19 e 0,06; os 10 restantes são os negativos desses valores. O gráfico de probabilidade normal que acompanha é razoavelmente reto. Uma suposição de normalidade da distribuição populacional é plausível.
Passo 2
b) Para um gráfico de probabilidade Weibull, os logs naturais das observações são plotados em relação aos percentis de valores extremos; estes percentis são -3,68, -2,55, -2,01, -1,65, -1,37, -1,13, -.93, -.76, -.59, -.44, -.30, -.16, -.02, . 12, 0,26, 0,40, 0,56, 0,73, 0,95 e 1,31. O gráfico de probabilidade que acompanha é aproximadamente tão direto quanto aquele para verificar a normalidade (um gráfico de ln(x) versus os percentis z, apropriado para verificar a plausibilidade de uma distribuição lognormal, também é razoavelmente direto - qualquer uma das 3 famílias diferentes de distribuições populacionais parece plausível).
Até a próxima, pessoal!
Resposta
No passos 1 e 2.