Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 4.Exercícios - Ex. 83

83. Construa um gráfico de probabilidade normal para a seguinte amostra de observações relativas à espessura da cobertura de tintas de baixa viscosidade (“Achieving a Target Value for a Manufacturing Process: A Case Study”, J. of Quality Technology, 1992, p. 22-26). Você se sentiria confortável ao estimar a média da espessura da população usando um método que assume uma distribuição de população normal?

0,83 0,88 0,88 1,04 1,09 1,12 1,29 1,31 1,48 1,49 1,59 1,62 1,65 1,71 1,76 1,83

Passo 1

Fala galerinha boa! Tudo bem com vocês? Vamos fazer mais um exercício.

Gráfico de probabilidade normal:

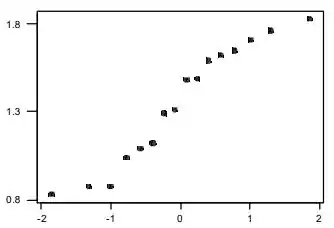
Os valores do percentil z são os seguintes: -1,86, -1,32, -1,01, -0,78, -0,58, -0,40, -0,24, -0,08, 0,08, 0,24, 0,40, 0,58, 0,78, 1,01, 1,30 e 1,86. O gráfico de probabilidade que acompanha é razoavelmente reto e, portanto, seria razoável usar métodos de estimativa que assumem uma distribuição populacional normal.

Até a próxima, pessoal!

Resposta

No passo 1.

Exercícios de Livros Relacionados

Suponha que a variável aleatória bidimensional (X,Y) seja uniformemente distribuída sobre o triângulo da Fig. 7.16. Estabeleça a fdp marginal de X e a de Y, e calcule V X eV Y .

Suponha que X e Y sejam variáveis aleatórias para as quais E X = μ x , E Y = μ y , V X = σ x ² ²e V Y = σ y ² ². Empregando o Teor. 7.7, obtenha uma aproximação de E(Z) e V(Z), onde Z = X Y .

Mostre que se X for uma variável aleatória contínua, com a fdp f tendo a propriedade de que o gráfico de f seja simétrico em relação a x=a, então E(X)=a, desde que E(X) exista.

Suponha que a variável aleatória bidimensional (X,Y) seja uniformemente distribuída sobre o triângulo da Fig. 7.15. Calcule V(X) e V(Y).

Suponha que a variável aleatória X tome os valores -1 e 1, cada um deles com probabilidade 1/2. Considere P X - E X ≥ k V X como uma função de k, k0. Em um gráfico, marque esta função de k e, no mesmo