Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 4.Exercícios - Ex. 84
84. O artigo “A Probabilistic Model of Fracture in Concrete and Size Effects on Fracture Toughness” (Magazine of Concrete Res., 1996, p. 311-320) fornece argumentos que explicam por que a distribuição de dureza de fratura em corpos de prova de concreto tem uma distribuição de Weibull, além de apresentar diversos histogramas de dados que parecem ajustados com curvas de Weibull superpostas. Considere a seguinte amostra de tamanho n 18 observações de dureza de concreto de alta resistência (consistente com um dos histogramas). Os valores de pi = (i - 0,5)/18 também são fornecidos.
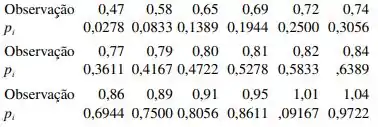
Construa um gráfico de probabilidade de Weibull e comente.
Passo 1
Fala galerinha boa! Tudo bem com vocês? Vamos fazer mais um exercício.
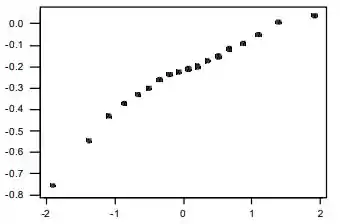
O gráfico de Weibull usa (observações) e os percentis z dos valores de pi dados. O gráfico de probabilidade que acompanha parece suficientemente reto para nos levar a concordar com o argumento de que a distribuição da tenacidade à fratura em corpos de prova de concreto poderia ser modelada por uma distribuição Weibull.
Até a próxima, pessoal!
Resposta
No passo 1.