Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 11.Problemas - Ex. 38b
Continuação do Problema 37.Outra maneira de estimar θ na uniforme é a seguinte. Considere M = max(X1, ..., Xn) = x(n), ou seja, o maior valor da amostra. Para qualquer valor de θ, M
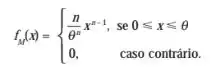
Considere o estimador T2= (n + 1)/n M; segue-se que T2 é não-viesado para θ, ou seja, E(T2) = θ. Calcule o erro quadrático médio de T2, EQM(T2) = E(T2– θ)² .
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para acharmos o EQM para o estimador. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser lembrar que, como T2 é não-viesado:
Passo 3
Pronto!! Agora é só analisarmos!!
Resposta
Exercícios de Livros Relacionados
Determine os valores das seguintes quantidades:a. t 0,1 , 15 b. t 0,05,15 c. t 0,05,25 d. t 0,05,40 e. t 0,005,40
Determine o valor crítico t que incluirá a área da curva t desejada em cada um dos casos a seguir:a. Área central = 0,95 , g l = 10 b. Área central = 0,95 , g l = 20 c. Área central = 0,99 , g l = 20
Uma amostra de 300 habitantes de uma cidade mostrou que 180 desejavam a fluoração da água. Encontrar limites de confiança para a proporção real de habitantes não favoráveis à fluoração, para:nível de
Numa pesquisa de opinião pública, entre 600 pessoas, 240 responderam sim a certa pergunta. Determinar o intervalo de confiança para a porcentagem populacional que deve responder sim, ao nível de confi
Numa cidade, entre 1.000 residências, 288 possuem televisão a cores. Determinar o intervalo de confiança para a proporção de possuidores de televisão a cores, nesta cidade, ao nível de significância d