Numa pesquisa de opinião pública, entre 600 pessoas, 240 responderam sim a certa pergunta. Determinar o intervalo de confiança para a porcentagem populacional que deve responder sim, ao nível de confiança de 95%.
Passo 1
Oi galerinha, estou animada pra fazer este exercício com vocês. Vem comigo!
Vamos relembrar que o intervalo de confiança é um intervalo em torno da estimativa por ponto, de modo que esse intervalo tenha uma probabilidade conhecida (que é designada por ) de conter o verdadeiro valor do parâmetro. O valor da probabilidade (), que usualmente assume os valores 90%, 95%, 98%, etc., é denominado nível de confiança e o valor é chamado nível de significância.
Para o intervalo de confiança para a proporção populacional (), temos o seguinte:
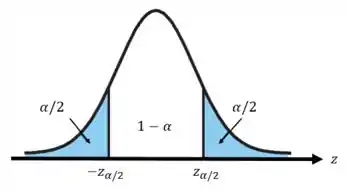
Do nosso enunciado , então:
Passo 2
Para o nível de confiança de 95%, temos:
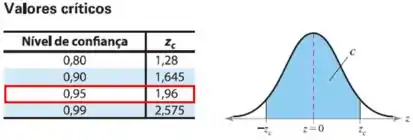
Sendo assim, para o nível de significância de 20%:
Tchau galerinha! Te espero em mais exercícios.
Resposta
.