Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 6.Exercícios - Ex. 3
Dada uma distribuição normal padrão, determine o valor de de modo que
(a) ;
(b)
(c) .
Passo 1
Vamos juntos resolver mais um exercício de probabilidade.
Vamos ao item a)
Nesse item ele nos dá exatamente a área a esquerda de k. E como sabemos o valor de área à esquerda de um determinado é tabelado.
Logo, precisamos só encontrar um k que nos dê a área do item a).
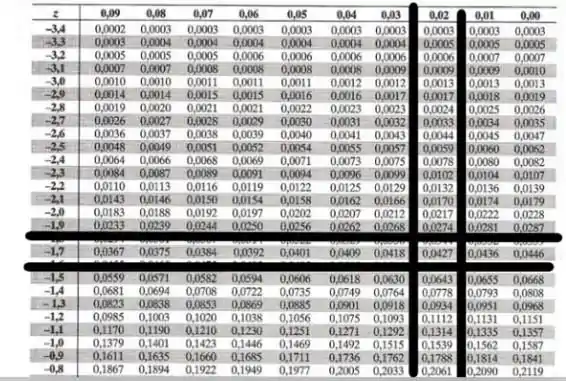
Fazendo isso, encontraremos
Passo 2
Agora, vamos ao item b).
Nesse item ele nos dá a área à direita de um determinado .
Para facilitar pra gente, usemos a seguinte relação:
Agora nós sabemos quanto vale a área à esquerda de , e podemos simplesmente procurar o valor tabelado, como no item a)
Desse modo, encontraremos
Passo 3
Por último, vamos ao item c).
Neste item ele nos dá a área entre dois parâmetros, são eles
Na nossa tabela nós conseguimos encontrar todos os valores tabelados para áreas à esquerda de um determinado, então vamos manipular o nosso problema para aparecer isso.
Manipulando a equação:
Nesse último passo eu simplesmente isolei a variável que eu quero e substitui um valor dado pelo enunciado e o outro que é simplesmente a área a esquerda de .
Ficando com a área à esquerda de , e nós sabemos que esse valor é tabelado então basta procurar um na tabela que satisfaça, tal área.
Encontraremos
Resposta
a)
b)
c)