Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 1.Exercícios Suplementares - Ex. 82

Os dados de amostra x 1   ,   x 2   ,   . . .   ,   x n algumas vezes representam uma série temporal, onde x t = valor observado de uma variável de resposta x no momento t . Frequentemente, a série observada mostra grande variação aleatória, o que dificulta o estudo do comportamento de longo prazo. Nessas situações, é desejável produzir uma versão suavizada da série. Uma das técnicas usadas é a suavização exponencial. O valor de uma constante de suavização α é escolhido ( 0 < α < 1 ) . Então, com x - t = valor ajustado no instante t , definimos x - t = x 1 e para t = 2 ,   3 ,   . . .   ,   n ,   x - t = α x t + ( 1 - α ) x - t - 1 .

a. Considere a seguinte série de tempo em que x t temperatura (°F) de efluente em uma estação de tratamento de esgoto no dia t: 47, 54, 53, 50, 46, 46, 47, 50, 51, 50, 46, 52, 50, 50. Plote cada coordenada x t em relação a t em um sistema bidimensional (um gráfico de série de tempo). Parece haver algum padrão?

b. Calcule o x - t usando 0,1. Repita, para 0,5. Que valor de fornece uma série x - t mais suavizada?

c. Substitua x - t = α x - t - 1 + ( 1 - α ) x - t - 2 no lado direito da expressão de x - t e então substitua x - t - 2 em termos de x - t - 2 , x - t - 3 e assim por diante. De quantos valores x t   ,   x t - 1   ,   . . . ,   x 1   ,   x - t depende? O que acontece ao coeficiente de x t - 1 quando k aumenta?

d. Consulte a parte (c). Se t for grande, qual é a sensibilidade de x - t em relação ao valor inicial x - t = x 1 ? Explique.

Passo 1

Falaaa, meu querido/minha querida. Como vai?? Para resolvermos essa questão vamos calcular os pontos pela equação que o enunciado nos deu e depois plotar eles em um gráfico. Bora lá!!!

Passo 2

A plotagem de cada coordenada pode ser analisada na imagem abaixo:

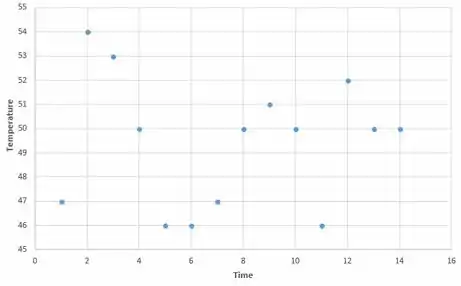
Logo, podemos notar um padrão cíclico.

Passo 3

Foi nos dada uma fórmula para quando 0 < α < 1 .

x - 1 = x 1

x - t = α x 1 + ( 1 - α ) x - t - 1

Sendo assim, para α = 0,1 temos:

x - 1 = 47

x - 2 = 0,1 x 2 + 1 - 0,1 x - 1 = 0,1 ∙ 54 + 1 - 0,1 ∙ 47 = 47,7

x - 3 = 0,1 x 3 + 1 - 0,1 x - 2 = 0,1 ∙ 53 + 1 - 0,1 ∙ 47 , 7 = 4 8,23

⋮

x - 14 = 0,1 x 14 + 1 - 0,1 x - 1 3 = 0,1 ∙ 5 0 + 1 - 0,1 ∙ 48,78 = 4 8,9

E para α = 0,5 temos:

x - 1 = 47

x - 2 = 0 , 5 x 2 + 1 - 0 , 5 x - 1 = 0 , 5 ∙ 54 + 1 - 0 , 5 ∙ 47 = 50,5

x - 3 = 0 , 5 x 3 + 1 - 0 , 5 x - 2 = 0 , 5 ∙ 53 + 1 - 0 , 5 ∙ 50,5 = 51,75

⋮

x - 14 = 0 , 5 x 14 + 1 - 0 , 5 x - 13 = 0 , 5 ∙ 50 + 1 - 0 , 5 ∙ 4 9,99 = 4 9,99

Plotando os pontos que encontramos, o gráfico é representado abaixo:

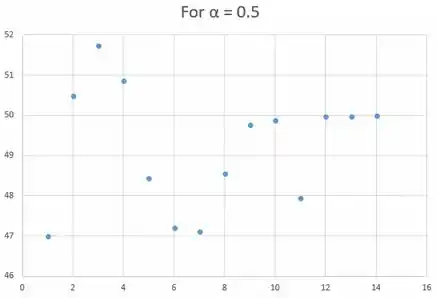
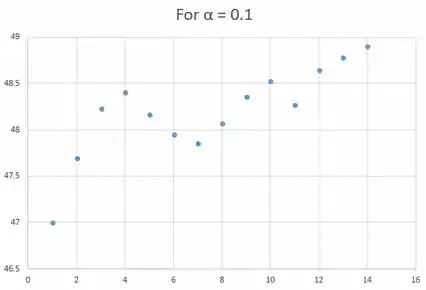
Logo, quando α = 0,1 teremos uma série mais suavizada.

Passo 4

Começando com x - t .

x - t = α x - t + ( 1 - α ) x - t - 1

= α x t + 1 - α α x t - 1 + 1 - α x - t - 2

= α x t + 1 - α α x - t - 1 + 1 - α 2 α x t - 2 + 1 - α x - t - 3

= …

= α x t + 1 - α α x t - 1 + 1 - α 2 α x t - 3 + … + 1 - α t - 2 α x 2 + 1 - α t - 1 x - 1

Quando k aumenta, os coeficientes diminuem. E o x - t depende de x t e de todos os valores anteriores.

Passo 5

Pela (c) podemos ver que não é sensível porque 1 - α t - 1 será muito pequeno.

Resposta

Resolução nos passos anteriores.

Exercícios de Livros Relacionados

Usando o Problema 3, verifique se há relações entre as variáveis rotatividade e salário.
Faça um experimento de simulação usando um pacote estatístico ou outro software para estudar a distribuição de X - quando a distribuição da população é Weibull com α = 2 e β = 5 , como no Exemplo 5.19
Faça um experimento de simulação usando um pacote estatístico ou outro software para estudar a distribuição de X - quando a distribuição da população é Weibull com α = 2 e β = 5 , como no Exemplo 5.19
Considere as observações numéricas x 1,. . . ,x n . Freqüentemente é de interesse saber se os x i estão (ao menos aproximadamente) distribuídos simetricamente ao redor de algum valor. Se n é pelo meno