Considere as observações numéricas . Freqüentemente é de interesse saber se os estão (ao menos aproximadamente) distribuídos simetricamente ao redor de algum valor. Se n é pelo menos moderadamente grande, a extensão da simetria pode ser avaliada por meio de um diagrama de caule e folha ou de um histograma. Entretanto, se n não for muito grande, esses gráficos não serão muito informativos. Considere a alternativa a seguir: seja o menor , o segundo menor e assim por diante. Faça então o gráfico dos seguintes pares como pontos em um sistema de coordenadas bidimensional: ... Há pontos em que n é par e em que é ímpar.
a. Qual é a aparência do gráfico quando há simetria perfeita dos dados? Qual sua aparência quando as observações se estendem mais acima do que abaixo da mediana (uma cauda superior longa)?
b. Os dados a seguir sobre precipitação (acre-pé) de 26 nuvens esparsas foram obtidos do artigo “A Bayesian Analysis of a Multiplicative Treatment Effect in Weather Modification” (Technometrics, 1975, p. 161-166). Construa o gráfico e comente sobre a extensão da simetria ou a natureza do seu desvio.
Passo 1
Falaaa, meu querido/minha querida. Como vai?? Para resolvermos essa questão vamos fazer algumas interpretações e depois plotar os gráficos. Bora lá!!!
Passo 2
Quando tiver simetria perfeita, quer dizer que as distâncias medianas são iguais.
Logo, os menores valores estão na mesma distância da mediana que os maiores e assim por diante.
Quando a observação está acima da mediana, temos:
Isso porque é mais distante da mediana do que . Significa que temos assimetria positiva nos dados e quando plotamos, o ponto cairia consideravelmente abaixo da linha .
Passo 3
Antes de criarmos o gráfico precisamos achar a mediana.
Como temos que é um número par, nós precisamos encontrar os seguintes valores ordenados.
Sendo definidos abaixo:
Logo, a média desses dois valores é a mediana.
Com a mediana, obtemos os seguintes pontos.
Logo, o gráfico indica uma inclinação substancial positiva, pois, os pontos estão bem abaixo de .
Passo 4
Por fim, os gráficos do exercício são representados por:
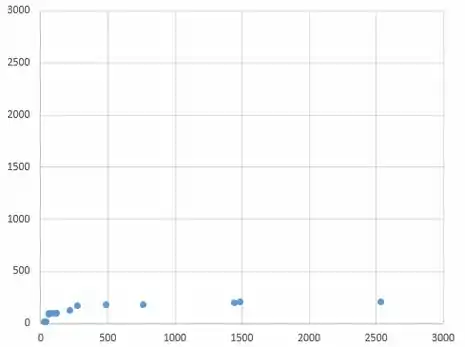
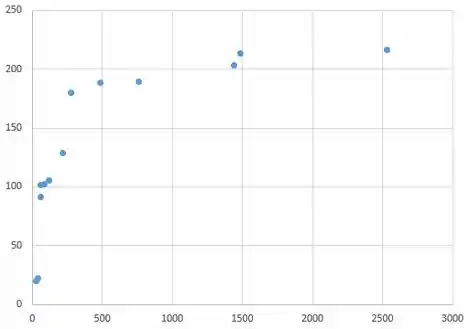
Resposta
Resolução nos passos anteriores.