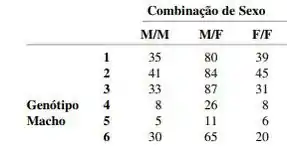
Os dados correspondentes às combinações de sexo de duas recombinações resultantes de seis diferentes genótipos masculinos aparecem no artigo "A New Method for Distinguishing Between Meiotic and Premeiotic Recombinational Events in Drosophila inelanogaster" (Genetics, 1979, p. 543-554). Tais dados suportam a hipótese de que a distribuição de frequência entre as três combinações de sexo é homogênea em relação aos diferentes genótipos? Defina os parâmetros de interesse, enuncie o e apropriados e realize as análises.

E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:

Tais dados suportam a hipótese de que a distribuição de frequência entre as três combinações de sexo é homogênea em relação aos diferentes genótipos? Defina os parâmetros de interesse, enuncie o e apropriados e realize as análises.

para é a hipótese de interesse, onde é a proporção do combinação de sexo resultante da genótipo. será rejeitado no nível. 10 se

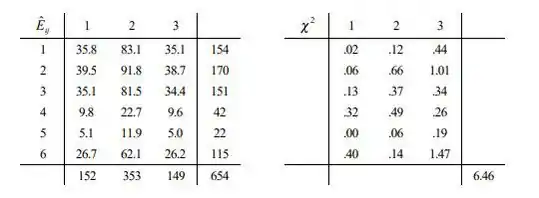
(carregar 2 casas decimais em produz ). Uma vez que não pode ser rejeitado no nível .10.