Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 14.Problemas - Ex. 4
Teste se os dados abaixo são observações de uma distribuição normal com média e
desvio padrão .
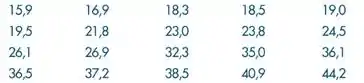
Passo 1
Vamos encontrar os quartis da .
Como temos observações, a frequência esperada para cada quartil é e, dessa forma, construímos a seguinte tabela:
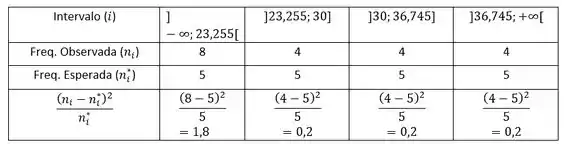
Passo 2
Vamos calcular a estatística do teste:
O valor crítico do teste é .
Resposta
Como , não rejeitamos a hipótese de que os dados são observações de uma distribuição .
Exercícios de Livros Relacionados
Um departamento de estatística de uma grande universidade mantém um serviço de acompanhamento para estudantes em seus cursos iniciais. O serviço foi organizado com a expectativa de que 40 % de seus cl
Criminologistas têm debatido com frequência se há uma relação entre as condições climáticas e a incidência de crime violento. O autor do artigo "Is There a Season for Homicide?" (Criminology, 1988, p.
O tempo de resposta de um sistema de computador a uma requisição para um determinado tipo de informação é concebido para ter distribuição exponencial com parâmetro λ = 1s (tal que se X = tempo de resp
a. Demonstre que outra expressāo para a estatística qui-quadrado é χ 2 = ∑ i = 1 k N i 2 n p n - n Por que é́ mais eficiente calcular χ ' utilizando esta fórmula?b. Quando a hipótese nula é H 0 : p
Um sistema de recuperação de informações tem dez localizações de armazenagem. A informação é armazenada com a expectativa de que, no longo prazo, a proporção de solicitações por localização i seja dad