Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 6.Exercícios - Ex. 83

Os dados mostrados na tabela 6.7 representam as vendas mensais de champanhe na França 1962-1969, em milhares de garrafas.

Construa um diagrama de séries temporais dos dados e comente qualquer característica dos dados que seja revelada por esse diagrama.

Pergunte-se como você usaria um procedimento gráfico para prever vendas mensais de champanhe para o ano de 1970.

Passo 1

Letra a:

Vamos fazer o gráfico digiponto:

O ano está no eixo horizontal e as vendas de champanhe no eixo vertical.

Vamos conectar os pontos de vezes consecutivas com uma linha reta.

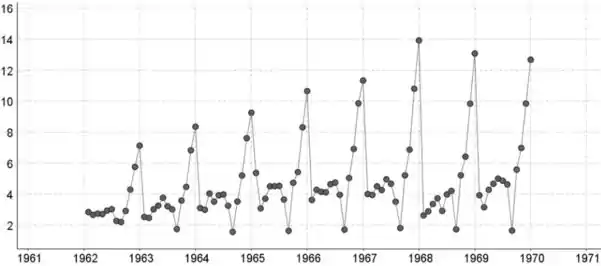
Parece haver um padrão crescente geral, porque o padrão no gráfico se inclina para cima.

Parece haver um padrão periódico, porque há picos em dezembro todos os anos.

Passo 2

Letra b:

A previsão para janeiro de 1970 pode ser melhor obtida plotando os dados para janeiro de 1962-1969. Esboce aproximadamente uma linha linear através desses pontos (ou determinar a equação de regressão linear de mínimos quadrados), o valor desta linha em é então a previsão para janeiro de 1970.

Repita o mesmo método para outros meses de 1970.

Resposta

Parece haver um padrão crescente geral, porque o padrão no gráfico se inclina para cima.

Parece haver um padrão periódico, porque há picos em dezembro todos os anos.

A previsão para janeiro de 1970 pode ser melhor obtida plotando os dados para janeiro de 1962-1969. Esboce aproximadamente uma linha linear através desses pontos (ou determinar a equação de regressão linear de mínimos quadrados), o valor desta linha em é então a previsão para janeiro de 1970.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma v.a. X tem distribuição normal, com média 100 e desvio padrão 10. Represente, num único gráfico, as distribuições de X e Xméd.

Distribuição amostral da diferença de duas proporções. Usando os resultados do Problema 32, qual seria a distribuição de p ^ 1 - p ^ 2 , a diferença entre as proporções de amostras independentes retir

Distribuição amostral da diferença de duas médias. Consideremos duas populações X com parâmetros μ 1eσ 1 2 e Y com parâmetros μ 2eσ 2 2 . Sorteiam-se duas amostras independentes: a da primeira populaç

Amostras sem reposição de populações finitas. Suponha uma população com N elementos. Vimos que se extrairmos uma amostra de tamanho n , com reposição, e calcularmos a média amostral X - , então E X -

Uma v.a. X tem distribuição normal, com média 100 e desvio padrão 10. Se X for a média de uma amostra de 16 elementos retirados dessa população, calcule P ( 90 X110 ) .