Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 6.Exercícios - Ex. 88
Reconsidere os dados do exercício 6.80. Construa gráficos de probabilidade normal para os dois grupos de dados: as 40 primeiras e as 40 últimas observações. Construa ambos os gráficos nos mesmos desejos. Que conclusões você pode tirar?
Passo 1
Vamos fazer as coisas pras primeiras 40 observações:
Os dados de viscosidade estão no eixo horizontal e o padrão dos valores normais estão no eixo vertical.
Se os dados contiverem n valores de dados, então os valores normais padronizadas são os valores na tabela III correspondente a uma área de (ou a área mais próxima) com
O menor valor padronizado corresponde ao menor valor de dados, o segundo menor valor padronizado corresponde ao segundo menor valor de dados e assim por diante.
Passo 2
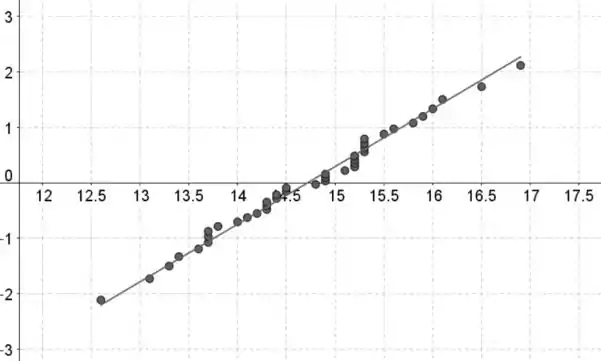
Passo 3
Vamos fazer as coisas pras segundas 40 observações:
Os dados de viscosidade estão no eixo horizontal e o padrão dos valores normais estão no eixo vertical.
Se os dados contiverem n valores de dados, então os valores normais padronizadas são os valores na tabela III correspondente a uma área de (ou a área mais próxima) com
O menor valor padronizado corresponde ao menor valor de dados, o segundo menor valor padronizado corresponde ao segundo menor valor de dados e assim por diante.
Passo 4
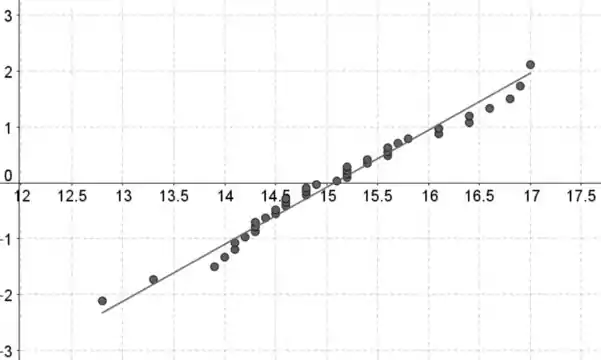
Ambas as distribuições de dados parecem ser aproximadamente normais, porque o padrão nos gráficos de probabilidade normal é meio linear.
Resposta
Ambas as distribuições de dados parecem ser aproximadamente normais.