Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 13
Os dados a seguir sobre x densidade da corrente (mA/cm2 ) e y taxa de deposição ((m)/min.) foram tirados do artigo “Plating of 60/40 Tin/Lead Solder for Head Termination Metallurgy” (Plating and Surface Finishing, janeiro de 1997, p. 38–40). Você concorda com a afirmação do autor desse artigo de que “uma relação linear foi obtida a partir da taxa de deposição de estanho–chumbo como uma função da densidade da corrente”? Explique seu raciocínio.
Passo 1
A partir dos dados fornecidos, estime a inclinação da linha de regressão pelo método dos mínimos quadrados para calcular o coeficiente de determinação.
A estimativa de mínimos quadrados do declive é
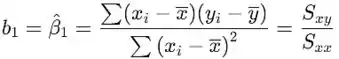
onde pode ser calculado pela fórmula
e pode ser calculado pela fórmula
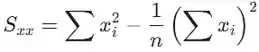
A estimativa de mínimos quadrados da interceptação é
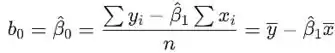
Passo 2
O número de observação é . Cada soma pode ser obtida da seguinte forma
Usando as somas, é
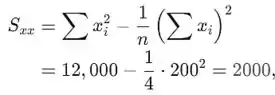
E é
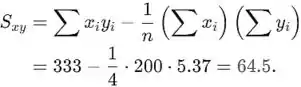
Assim, a estimativa da inclinação pode ser calculada como
A estimativa do intercepto não precisa ser computada para esta análise.
O coeficiente de determinação, , é
A fórmula computacional para SSE é
A soma total dos quadrados é
Soma total dos quadrados, é
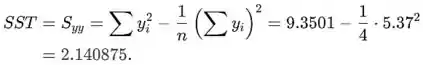
Pela fórmula computacional erro soma dos quadrados é
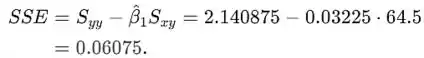
Passo 3
O coeficiente de determinação é
O coeficiente de determinação é próximo de 1, o que confirma a afirmação de que existe uma forte relação linear entre as variáveis. A resposta é: há relação linear entre as duas variáveis.
O gráfico de dispersão sugere que existe uma forte relação linear entre as variáveis. A linha apresentada no gráfico de dispersão é a linha de regressão.
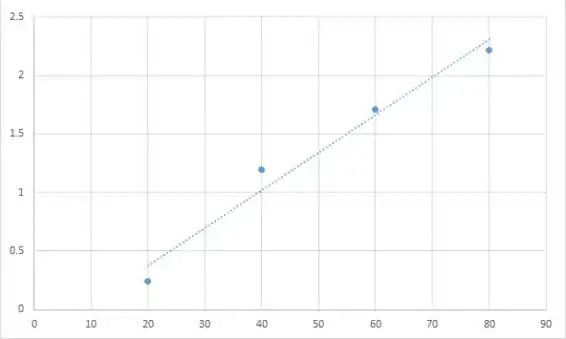
Resposta
Existe uma relação linear entre as duas variáveis