Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 14

Refira-se aos dados sobre temperatura do tanque–taxa de eficiência do Exercício 1. a. Determine a equação da reta de regressão estimada. b. Calcule uma estimativa pontual da taxa de eficiência média real quando a temperatura do tanque é 182

c. Calcule os valores dos resíduos da reta de mínimos quadrados das quatro observações para as quais a temperatura é 182. Por que nem todas têm o mesmo sinal? d. Que proporção da variação observada na taxa de eficiência pode ser atribuída à relação de regressão linear simples entre as duas variáveis?

Passo 1

  1. Encontraremos X ∙ Y e X 2 como foi feito na tabela abaixo.

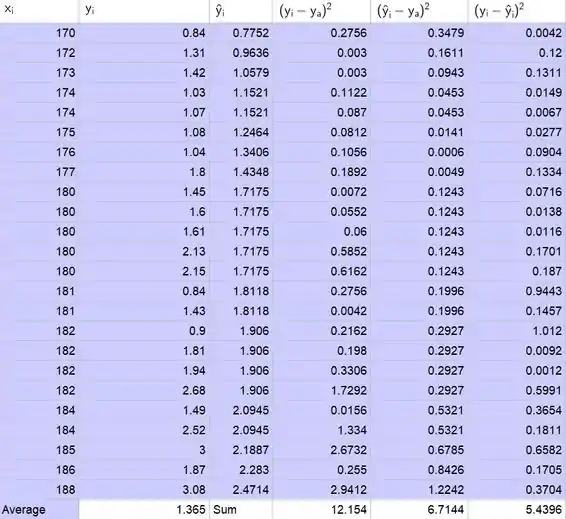
    2. Encontre a soma para cada coluna:

    ∑ x = 4308 ,   ∑ Y = 40.09 ,   ∑ X ∙ Y = 7243.65 ,   ∑ X 2 = 773790

    Use as seguintes equações para encontrar a e b

    a = ∑ Y ∙ ∑ X 2 - ∑ X ∙ ∑ Y X n ∙ ∑ X 2 - ∑ X 2 = 40.09 ∙ 773790 - 4308 ∙ 7243.65 24 ∙ 773790 - 4308 2 ≈ - 15.245

    b = n ∙ ∑ X Y - ∑ X ∙ ∑ Y X n ∙ ∑ X 2 - ∑ X 2 = 24 ∙ 7243.65 - 4308 ∙ 40.09 24 ∙ 773790 - 4308 2 ≈ 0.094

    substitua a e b na fórmula da equação de regressão

    y = a + b x

    y =   - 15.245 + 0.094 x

  2. Substitua x na equação de regressão por 182 e avalie

    3. y ^ = - 15.245 + 0.094 182 = 1.9060

    Assim, a eficiência média real prevista é 1.9060.

    Passo 2

  3. O resíduo é a diferença entre o valor y observado e o valor y previsto

    4. R e s i d u a l = y - y ^ = 0.9 - 1.9060 = - 1.0060

    R e s i d u a l = y - y ^ = 1.81 - 1.9060 = - 0.0960

    R e s i d u a l = y - y ^ = 1.94 - 1.9060 = - 0.0340

    R e s i d u a l = y - y ^ = 2.68 - 1.9060 = 0.7740

    Eles não têm todos o mesmo sinal, porque o valor previsto da parte (b) é aproximadamente a média dos valores y reais, de modo que alguns valores y previstos estão abaixo do valor médio previsto e alguns valores y previstos serão acima dela, o que faz com que os diferentes sinais dos resíduos

  4. Determine os valores previstos para todos os x i dados valores.

Determine a diferença quadrada entre os valores y observados e a média dos valores y.

Determine a diferença quadrada entre os valores y previstos e a média dos valores y.

Determine a diferença quadrada entre os valores y observados e os valores y previstos.

Passo 2

Resultados da tabela:

S S T =   ∑ y i - y - 2 = 12.1540

S S R =   ∑ y i - y - 2 = 6.7144

S S E =   ∑ y i - y - 2 = 5.4396

O coeficiente de determinação é a razão de SSR e SST:

r 2 = S S R S S T = 6.7144 12.1540 = 0.4514 = 45.14 % %

Isso significa que 45,14% da variação observada no índice de eficiência pode ser atribuída à relação de regressão linear simples entre as duas variáveis

Resposta

  1. y ^ = - 15.245 + 0.094 x
  2. 1.9060
  3. - 1.0060 , - 0.0960,0.034,0.7740
  4. 45,14% da variação observada no índice de eficiência pode ser atribuída à relação de regressão linear simples entre as duas variáveis

Exercícios de Livros Relacionados

Na Seção 12.4, apresentamos uma fórmula para V( ˆ 0 ˆ 1x*) e um IC para 0 1x*. Tomando x* 0, obtemos 2 ˆ 0 e um IC para 0. Use os dados do Exemplo 12.11 para calcular o desvio padrão estimado de ˆ 0 e
Processos normais de criação de peixes em aquaculturas inevitavelmente deixam os peixes estressados, o que pode influenciar negativamente no crescimento, na reprodução, na qualidade da carne e na susc
Na biofiltragem de esgoto, o ar descarregado de uma ins-talação de tratamento passa através de uma membrana porosa úmida que faz com que os contaminantes dissolvam-se na água e sejam transformados em
Reconsidere a situação do Exercício 68, no qual x = % de entrada térmica de RDF e y = % de eficiência de uma determinada caldeira foram relacionadas por meio de um modelo de regressão linear simples.
O artigo “Evaluating the BOD POD for Assessing Body Fat in Collegiate Football Players” (Medicine and Science in Sports and Exercise, 1999, p. 1350–1356) relata um novo dispositivo de deslocamento de