Um departamento de estatística de uma grande universidade mantém um serviço de acompanhamento para estudantes em seus cursos iniciais. O serviço foi organizado com a expectativa de que de seus clientes seria do curso de estatística de negócios, de estatística de engenharia, do curso de estatística para estudantes de ciências sociais e outros para o curso de estudantes de agricultura. Uma amostra aleatória de clientes revelou e 9 dos quatro cursos. Estes dados sugerem que as porcentagens nas quais o curso foi baseado não estão corretas? Defina e teste a hipótese relevante utilizando .

E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:

Usando o número 1 para negócios, 2 para engenharia, 3 para ciências sociais e 4 para agricultura, seja a proporção real de todos os clientes da disciplina i. Se as expectativas do departamento de Estatística estiverem corretas, então a hipótese nula relevante é , versus As expectativas do departamento de Estatística não estão corretas. Com d.f=k-1=4-1=3, rejeitamos se. Usando as proporções em , o número esperado de clientes é:

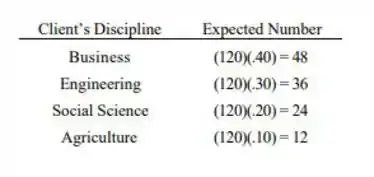
Como todas as contagens esperadas são de pelo menos 5 , o teste do qui-quadrado pode ser usado. O valor da estatística de teste é , então não rejeitamos . (Alternativamente, valor ) que é >.10, e como o valor-p não é <.05 rejeitamos xmlns="http://www.w3.org/1998/Math/MathML"> H 0 ). Assim, não temos evidências que sugiram que as expectativas do departamento de estatística estejam incorretas.