Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.6 - Ex. 26
Deseja-se verificar se o modelo Uniforme Discreto com valores de 0 a 5 pode ser usado para modelar o número de reclamações que chegam por hora a uma Central de Atendimento ao consumidor. O sorteio de 120 períodos de uma hora forneceu os seguintes dados:
Formule as hipótese testadas e dê a conclusão ao nível de 5% de significância.
Passo 1
Nessa questão, temos de realizar o que chamamos de “Teste de aderência”, nada mais é do que uma artimanha para ver se os valores coletadas estão de acordo com um determinado modelo.
Vamos definir quem é a variável que estamos estudando:
E então, queremos testar:
O teste será feito aproximado por uma distribuição , da seguinte forma:
Onde representa a quantidade de categorias, no nosso caso categorias. E é a frequência observada para cada categoria.
Já o é a frequência ESPERADA para cada categoria se essa variável realmente tivesse a distribuição sugerida; ou seja, temos de encontrar esse valor.
Passo 2
Então vamos começar exatamente por aí, obtendo os valores esperados; mas lembrando que no modelo Uniforme, temos:
Como nosso :
E pasme... essa vai ser a frequencia esperada em cada categoria.
Montando a tabelinha:
Passo 3
Com isso podemos calcular:
Agora precisamos da Região crítica, considerando :
Portanto:
Então na tabela devemos buscar a coluna que representa 5% e a linha que nos da graus de liberdade:
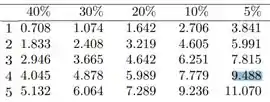
Ou seja,
Como nosso pertence bastante à região crítica, rejeitamos .
Resposta
Concluímos que o modelo proposto não é válido para representar as reclamações recebidas por hora na Central de atendimento.