Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.6 - Ex. 27
Uma indústria registra, em cada semana, o número de dias em que ocorrem acidentes de trabalho. Para uma amostra de 200 semanas, verifique se os dados apresentados a seguir, aderem ao modelo Binomial com parâmetros e (use um nível de significância de ).
Passo 1
Temos, neste exercício, mais um teste de aderência; queremos verificar se o modelo binomial realmente é adequado para a variável:
Portanto teremos o seguinte teste:
O teste será feito aproximado por uma distribuição , da seguinte forma:
Onde representa a quantidade de categorias, no nosso caso categorias. E é a frequência observada para cada categoria.
Já o é a frequência ESPERADA para cada categoria se essa variável realmente tivesse a distribuição sugerida; ou seja, temos de encontrar esse valor.
Passo 2
Então vamos começar obtendo essas frequências esperadas:
Se você recordar bem, um modelo binomial calculamos assim as probabilidades:
Onde:
Lembrou aí? Taca-lhe pal então:
Você pode estar se perguntando o porquê de multiplicarmos aqueles 200 ali!? Pois bem, se a probabilidade está falando assim “a chance de termos zero acidentes em UMA SEMANA”, já que definimos a nossa variável como sendo o nº de acidente em uma única semana; com isso a amostra foi feita tomando 200 semanas, então multiplicamos para estabelecer uma relação de proporcionalidade, “se temos de chance de termos 0 acidentes em uma semana, em duzentas semanas teremos .
Fazendo isso para todas as 5 categorias, chegamos na seguinte tabelinha:
Mas, presta bem atenção aqui agora... não podemos trabalhar com uma frequência esperada menor do que 5, então teremos que “fundir” as três últimas categorias; Estranho né?! Vê se olhando na nova tabela clarifica um bocado:
Foi mais ou menos??
Agora tem um detalhe, lembra que nossos graus de liberdade eram , com representando o número de categoria?até então tínhamos , mas acabamos de fazer um “corte” e abrimos mão de uma categoria, ao fazer isso gente alterou o número de categorias, consequentemente vamos também ter de mudar a quantidade de graus em liberdade, agora teremos g.l.
Chato pakas né?! Mas fé no pai...
Passo 3
Agora, temos que calcular o sob :
Para concluir o teste, precisamos ver se este valor está ou não dentro da zona crítica:
Definindo , temos o seguinte:
Ou seja, vamos na tabela de distribuição Qui-quadrado e olhar na coluna que representa 10%, na linha de 4 graus de liberdade:
Certo? Nãããoo... alteramos os graus de liberdade lembra?! Pay attention!
Vamos buscar na linha que representa 3 graus de liberdade:
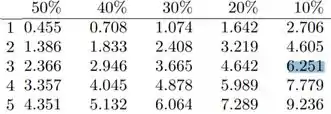
Portanto:
Então , com isso a região crítica assume a seguinte forma:
Niitidamente você já deve ter percebido que o valor que obtivemos de está dentro da RC, e não é pouco dentro não.
Portanto, devemos rejeitar a hipótese nula, e concluir que o modelo Binomial não é adequado para estudar essa variável.
Resposta
Concluímos que o modelo Binomial com não é um bom modelo para representar o nº de acidentes em uma semana na indústria.