Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 3.Exercícios - Ex. 68

Um diretor de pessoal que entrevistará 11 engenheiros seniores para quatro cargos marcou seis entrevistas para o primeiro dia e cinco para o segundo. Assuma que os candidatos serão entrevistados em ordem aleatória. a. Qual é a probabilidade de x dos quatro melhores candidatos serem entrevistados no primeiro dia? b. Dos quatro melhores candidatos, quantos podem ser esperados para entrevistas no primeiro dia?

Passo 1

  1. Proposição: Suponha que a população tenha M sucessos (S), N-MN−M falhas (F). Se a variável aleatória X é

    2. X   =   n ú m e r o   d e   s u c e s s o s   e m   u m a   a m o s t r a   a l e a t ó r i a   d e   t a m a n h o   n ,

    então tem função massa de probabilidade

    h x ; n , M , N = P X = x =   M x N - M n - x N n

    para todos os inteiros x para os quais

    max ⁡ 0 ,   n - N + M ≤ x   ≤ min ⁡ n , M

    no nosso caso, um sucesso é que x dos candidatos selecionados para o trabalho (top candidatos) são entrevistados no primeiro da, e há

    M = 6

    candidatos entrevistados no primeiro dia. Também,

    N - M = 11 - 6 = 5

    max ⁡ 0,4 - 11 + 6 ≤ x   ≤ min ⁡ n , M ;

    max ⁡ 0 , - 1 ≤ x   ≤ min ⁡ 4,6 ;

    0 ≤ x ≤ 4

    podemos concluir que a variável aleatória X tem distribuição hipergeométrica, com pmf

    h ( x ; 4,6 , 11 = P X = x =   6 x 11 - 6 4 - x 11 4

    para x   ϵ   0,1 , 3,4 e zero para todos os outros valores de x.

    A seguir estão as probabilidades que precisamos

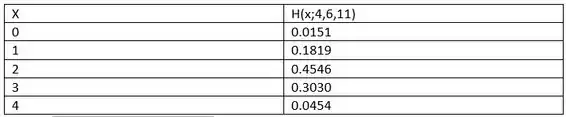
    Passo 2

  2. Só precisamos encontrar o valor esperado da variável aleatória XX.

Proposição: O seguinte é verdadeiro para a variável aleatória X com distribuição hipergeométrica e h(x;n,M ,N)

E X = n ∙ M N

V X = N - n N - 1 ∙ n ∙ M N 1 - M N

Da proposição, temos

E X = n ∙ M N = 4 ∙ 6 11 = 2.18

Ou podemos dizer que podemos esperar que dois candidatos sejam entrevistados no primeiro dia dos quatro principais candidatos.

Resposta

  2. E X = 2.18   c a n d i d a t o s

Exercícios de Livros Relacionados

Seja X a duração da vida (medida em horas) de um dispositivo eletrônico. Suponha que X seja variável aleatória contínua com fdp f x = k x n ,2000 ≤ x ≤ 10000 . P a r an = 3 ,d e t e r m i n ek .
Suponha que X seja uniformemente distribuída sobre - α ,α , onde α0 . Quando possível, determine α de modo que as seguintes relações sejam satisfeitas:. f x = 1 b - a = 1 2 a F X = x + a 2 a P X1 2 =
Suponha que X seja uniformemente distribuída sobre - α ,α , onde α0 . Quando possível, determine α de modo que as seguintes relações sejam satisfeitas:. f x = 1 b - a = 1 2 a F X = x + a 2 a P x1 = 1
Seja X uma variável aleatória com distribuição binomial, baseada em 10 repetições de um experimento. Se p=0,3, calcule as seguintes probabilidades, empregando a tábua da distribuição binomial do Apênd
Seja X a duração da vida (medida em horas) de um dispositivo eletrônico. Suponha que X seja variável aleatória contínua com fdp f x = k x n ,2000 ≤ x ≤ 10000 . Q u a lap r o b a b i l i d a d ed eq u