Enunciado

Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 9.Exercícios propostos - Ex. 16c

Com elementos de uma população obtivemos: , e ; com elementos de outra população obtivemos: , e . Determinar os intervalos de confiança para:

, com .

Passo 1

Oi galera, vamos lá!

O valor da probabilidade (), que usualmente assume os valores 90%, 95%, 98%, etc., é denominado nível de confiança e o valor é chamado nível de significância.

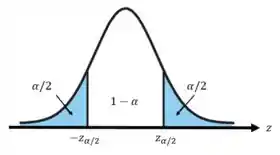
Para o intervalo de confiança para a proporção populacional (), temos o seguinte:

Do enunciado, temos os seguintes dados:

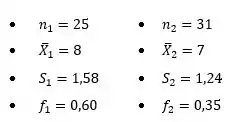
Passo 2

Pela tabela de distribuição normal reduzida, com nível de confiança de 95%:

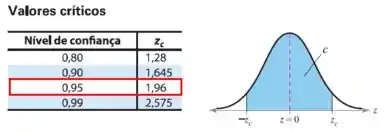
Passo 3

Sendo assim, o intervalo de confiança da proporção da amostra 1, é:

Tchau galerinha! Te espero em mais exercícios.

Resposta

Exercícios de Livros Relacionados

Realize os cálculos sugeridos ao final do Ex. 12.5.

Ao mensurar-se T, a duração da vida de uma peça, pode-se cometer um erro, o qual se pode admitir ser uniformemente distribuído sobre (- 0,01, 0,01). Por isso, o tempo registrado (em horas) pode ser re

Suponha-se que 30 dispositivos eletrônicos, D1,... , D30, sejam empregados da seguinte maneira: Tão logo D1 falhe, D2 entra em operação; quando D2 falhar, D3 entrará em operação etc. Suponha que a dur

Suponha que Xi,, i = 1, 2, .. . , 50 sejam variáveis aleatórias independentes, cada uma delas tendo distribuição de Poisson com parâmetro λ=0,03 . Faça S=X1 + ... + X50. Empregando o Teorema do Limite