Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 10.Exercícios propostos - Ex. 1
Uma amostra de 10 elementos apresentou . Sabe-se que a variância da população é igual a 160. Testar a hipótese de , contra a alternativa , ao nível de 10%.
Passo 1
Olá galerinha, vamos resolver este exercício de acordo com o passo a passo dos testes de hipóteses.
Então primeiramente iremos definir nossa hipótese nula () e alternativa ():
- ;
- .
E pelo enunciado sabemos que nosso nível de significância é e o teste é unilateral à direita:
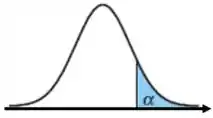
Passo 2
Como a variância populacional é conhecida, podemos utilizar a tabela da distribuição normal:
Porém esse encontrado, é para a área a esquerda, então para a área a direita:
- Se aceita ;
- Se rejeita .
Passo 3
Agora iremos calcular nosso valor , pela seguinte equação:
Sendo que:
- ;
- ;
- ;
- .
Logo:
Como (), então rejeitamos .
Tchau pessoal, até mais!
Resposta
rejeita .
Exercícios de Livros Relacionados
Numa indústria deseja-se testar se a produtividade média dos operários do período diurnoé igual à produtividade média dos operários do período noturno. Para isso, colheram-seduas amostras, uma de cada
A receita média, em porcentagem, dos quase 600 municípios de um estado tem sido 7%. Ogoverno pretende melhorar esse índice e, para isso, está estudando alguns incentivos. Paraverificar os efeitos dess
Deseja-se verificar se o número de falhas de comunicação, em uma central de telefonia celular, segue o modelo Poisson com λ = 10 falhas/dia. Discuta um procedimento para decidir sobre a aceitação ou n
Para decidir sobre o vicio de uma moeda, são feitos 100 lançamentos e o número de caras é contado. Aceita-se o equilíbrio da moeda se obtermos entre 45 e 50 caras, caso contrário, a moeda é considerad
Um fabricante afirma que sua vacina previne 80 % dos casos de uma certa doença. Um grupo de médicos desconfia que a vacina não é tão eficiente assim. Você poderia ajudá-los e indicar como resolver a q