Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 9.Exercícios propostos - Ex. 14

Numa pesquisa de possuidores de carros numa universidade, entre homens e mulheres, foram obtidos: 24 de 100 homens possuem automóveis e 13 de 100 mulheres possuem automóveis. Determinar, ao nível de 99% de confiança, o intervalo para a diferença entre as proporções de homens e mulheres que possuem automóveis.

Passo 1

Oi galera, vamos lá!

O valor da probabilidade ( 1 - α ), que usualmente assume os valores 90%, 95%, 98%, etc., é denominado nível de confiança e o valor α é chamado nível de significância.

Quando os valores de p 1 e p 2 são desconhecidos, eles podem ser estimados por f 1 e f 2 , desde que os tamanhos das amostras sejam maiores que 60:

p 1 ± p 2 = f 1 ± f 2 ± z α / 2 ∙ f 1 ∙ ( 1 - f 1 ) n 1 + f 2 ∙ ( 1 - f 2 ) n 1

Do enunciado, temos os seguintes dados:

  • f h = 2 4 / 100 = 0,24 ;
  • f m = 13 / 100 = 0,13 ;
  • n = n 1 = n 2 = 100 ;
  • α = 0,0 1 .

Para um nível de confiança de 99%:

z c = 2 , 575

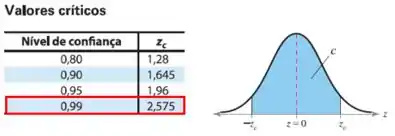
Passo 2

Sendo assim, temos:

p h - p m = 0,24 - 0,13 ± 2,575 ∙ 0,24 ∙ ( 1 - 0,24 ) 100 + 0,13 ∙ ( 1 - 0,13 ) 100

- 3 % ≤ p h - p m ≤ 25 %

Até mais pessoal!

Resposta

- 3 % ≤ p h - p m ≤ 25 % .

Exercícios de Livros Relacionados

Considere e teste de impacte Izod descrito no Exercicio 8.24. Calcule um intervalo de tolerância de 99% para a resisténcia ao impacto de tubos de PVC que tem um nivel de confianca de 90%. Compare o co
Considere os dados de diâmetro de Exercicie 8.34. Calcule um intervalo de telerancia de 95% para o diâmetro des bastecs descrites que tem um nivel de confiança de 90%. Compare 0 comprimento de interva
Considere os dados de brilho da televisão do esxercicio 8.31. Calcule um intervalo de telerancia de 99% para o brilh dos tubos de imagem de televisao que tem um nivel de cenflanca de 95%. Compare o co
Considere es dados de enriquecimente de bastocs de cembustivel de exercicio 8.37. Calcule um intervalo de telerancia de 99%, para 0 enriquecimente des bastecs que tem um nivel de centianca de 95% .Com
Considere es dados de chuva de Exercicie 8-29. Calcule um intervalo de telerancia de 95% que tem um nivel de confiança de 95%. Compare o comprimento de intervalo de telerancia com o comprimento de 10