Uma empresa mantém três escritórios em certa região, cada um com dois funcionários. As informações sobre os salários anuais (milhares de dólares) seguem abaixo:
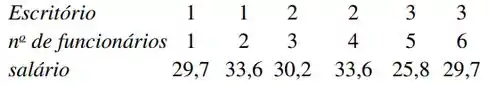
a. Suponha que dois desses funcionários sejam selecionados aleatoriamente, dentre os seis (sem reposição). Determine a distribuição da amostragem do salário médio da amostra.
b. Suponha que um dos três escritórios seja selecionado aleatoriamente. Sejam e os salários dos dois funcionários. Determine a distribuição de .
c. Como das partes (a) e (b) é comparado ao salário médio da população ?
Passo 1
Falaaa, meu querido/minha querida. Como vai?? Para resolvermos esse exercício vamos precisar montar algumas tabelas baseadas na tabela do enunciado, basta fazer algumas interpretações que acharemos cada probabilidade pedida. Bora lá!!
Passo 2
O salário médio da amostra é a soma de todos os valores dividido pelo número de valores, para cada amostra de 2 funcionários.
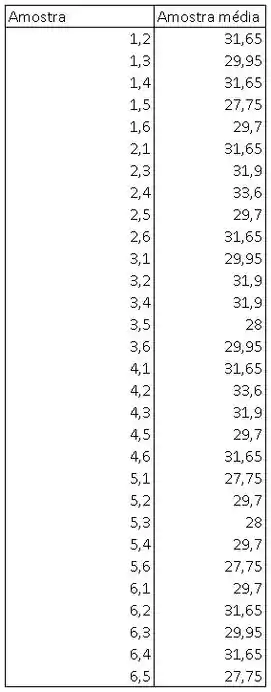
Então, a distribuição da amostragem é representada como o número de vezes que cada média amostral ocorre e a probabilidade correspondente:
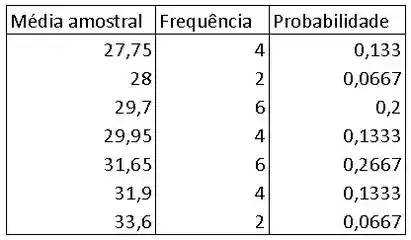
Passo 3
Semelhante a letra (a), o salário médio da amostra (soma de todos os valores dividido pelo número de valores) para cada amostra contendo, agora, 1 cargo:

E a distribuição, então fica:
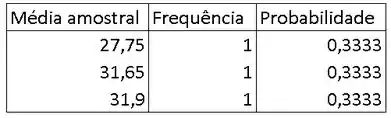
Passo 4
O valor esperado é a soma do produto de cada possibilidade com sua probabilidade.
Para a letra (a)
Para a letra (b)
Por fim a média da população é a soma de todos os valores divido pelo número de valores:
Portanto, concluímos que os valores esperados da (a) e da (b) são iguais ao salário médio da população.
Resposta
Resolução nos passos anteriores.