Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 2.3 - Ex. 49
Encontrando a média de uma distribuição de frequência. Nos exercícios 49 a 52, aproxime a média da distribuição de frequência.
49. Economia de combustível - A distância percorrida na estrada (em milhas por galão) para 30 carros pequenos.
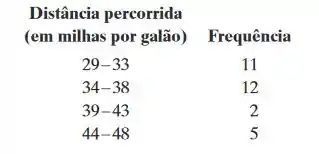
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
O ponto médio é a média dos limites, portanto, a soma dos dois limites é dividida por 2
Agora, vamos determinar a soma de todos as frequências
A média da distribuição de frequência é a soma dos produtos dos pontos médios e as frequências correspondentes, dividida pela soma das frequências
Substituindo os termos, nós temos que
Com isso, a média é igual a
Resposta
Exercícios de Livros Relacionados
Mostre que:( a ) sum_(i = 1)^n (x_i - overset(-)(x)) = 0 ( b ) sum_(i = 1)^n (x_i - overset(-)(x))^2 = sum_(i = 1)^n x_i^2 - n overset(-)(x)^2 = sum_(i = 1)^n x_i^2 - ((sum x)^2)/(n) ( c ) sum_(i = 1)
Os dados abaixo representam as vendas semanais, em classes de salários mínimos, de vendedores de gêneros alimentícios: ( a ) Faça o histograma das observações. ( b ) Calcule a média da amostra, x - .
Usando os resultados da questão anterior, calcule as variâncias dos Problemas 1 e 2 deste capítulo.
A distribuição de freqüências do salário anual dos moradores do bairro A que têm alguma forma de rendimento é apresentada na tabela abaixo: ( a ) Construa um histograma da distribuição. ( b ) Qual a m
Encontrando escores - z . A distribuição das idades dos vencedores do Tour de France de 1903 a 2012 é aproximadamente em forma de sino. A idade média é 28,1 anos, com desvio padrão de 3,4 anos.(a) tra