Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 3.Problemas - Ex. 24
A distribuição de freqüências do salário anual dos moradores do bairro que têm alguma forma de rendimento é apresentada na tabela abaixo:
Construa um histograma da distribuição.
Qual a média e o desvio padrão da variável salário?
O bairro apresenta, para a mesma variável, uma média de e um desvio padrão de . Em qual dos bairros a população é mais homogênea quanto à renda?
Construa a função de distribuição acumulada e determine qual a faixa salarial dos mais ricos da população do bairro.
Qual a “riqueza total” dos moradores do bairro?
Passo 1
Bom galera, vamos começar construindo um histograma da distribuição do salário anual:
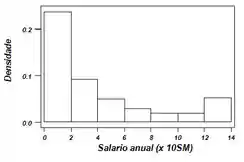
Passo 2
Show de bola, agora vamos calcular a média e o desvio padrão do salário, começando pela média:
O desvio padrão é um pouco mais chatinho, mas bora lá:
A gente vai usar a raiz quadrada da variância, pra isso vamos calcular a variância:
Assim o desvio padrão é:
E como o desvio padrão do bairro é menor que a do bairro , o salário da população de é mais homogênea.
Passo 3
Belezinha, agora vamos construir uma tabela de distribuição acumulada:
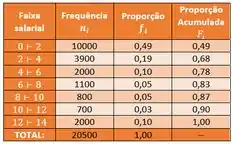
E com isso, a gente nota que os mais ricos da população são os que tem faixa salarial de e salários mínimos anuais.
Passo 4
Por fim, a gente calcula a riqueza total da população do bairro, é chatinho, mas é fácil, assim:
Beleza?! 😊
Resposta
;