Os dados abaixo representam as vendas semanais, em classes de salários mínimos, de vendedores de gêneros alimentícios:

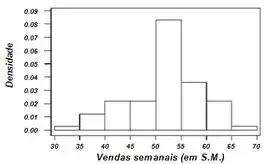
Faça o histograma das observações.

Calcule a média da amostra, .

Calcule o desvio padrão da amostra, .

Qual a porcentagem das observações compreendidas entre e ?

Calcule a mediana.

Show de bola, então vamos calcular agora a média, isso é muito fácil:

Belezinha, o desvio padrão como a gente já sabe é a raiz quadrada da variância, então, vamos calcular a variância:

Logo, o desvio padrão é:

Calma, tá quase acabando, agora, temos que:

E também:

Então, para encontramos a porcentagem que isso representa, a gente vai ter que fazer regra de três, bora lá:

E:

Assim, o intervalo tem:

Por fim, a gente encontra a mediana que no caso é a média dos elementos e , que no caso, ambos estão no intervalo de , logo, consideramos a mediana: