Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.6 - Ex. 32
Em uma escola de ensino médio, o desempenho dos alunos em matemática e física foi observado (ver tabela a seguir) para testar se existe dependência entre as duas disciplinas.
Calcule o nível descritível. Qual a decisão, ao nível de significância de 2% ?
Passo 1
Beleza, antes de qualquer coisa perceba que queremos testar a dependência entre as duas variáveis:
E
então teremos o seguinte teste de hipótese:
É o que chamamos de “Teste de independência”. Ahvá!
Beleza, mas como funciona esse rolê? É o seguinte, vamos precisar encontrar um valor esperado para cada CÉLULA, ou seja:
E assim por diante, fazendo um arranjo das linhas e colunas. Chato pakas né?! Mas ainda piora...
Depois de fazer isso vamos precisar usar a aproximação pela Qui-Qadrado e calcular:
Onde e representam as linhas e colunas respectivamente com graus de liberdade e é exatamente o valor dado em cada célula. Bugou aí? Mas calma, vamos juntos!
Passo 2
Vamos encontrar os valores esperados em cada célula então:
Com isso podemos montar uma tabelinha com esses valores:
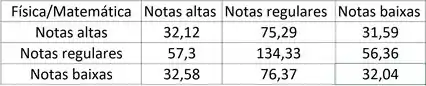
Agora podemos calcular:
Deu isso aí também?? Espero que sim!
Passo 3
Agora, precisamos só obter o nível descritível que, se você lembrar, nada mais é do que a chance de eu ter um valor tão mais extremo quanto o que eu acabei de encontrar, ou seja:
É isso que precisamos buscar na tabela de distribuição Qui-quadrado; a probabilidade de termos um valor maior do que , buscando na linha de graus de liberdade:
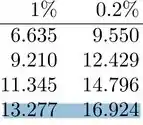
Dependendo da tabela que você tiver em mãos terá que fazer interpolação, isso porque o valor que você procura estará “nas entrelinhas”(perceba que 14,23 está entre aqueles valores destacados).
lembrando como funciona isso:
E aí é só isolar o .
Calma que ainda não acabou, tamo quase lá!
Portanto acabamos de encontrar o nível descritível:
Outra coisa que você tem que se lembrar é como interpretar esse tal nível, sabemos que se ele for muito pequeno, muito provavelmente será falsa.
Beleza fera, mas pequeno quanto??
Aí entra o nível de significância:
Se então rejeitamos a hipótese nula
Se então aceitamos a hipótese nula
Agora sim podemos concluir, uma vez que o enunciado nos deu , e nosso então devemos REJEITAR .
Resposta
Com muito sacríficio encontramos um e rejeitamos , portanto temos motivos para crer que as duas matérias apresentam sim dependência.