Enunciado
Probabilidade e Estatística - Probabilidade, um curso moderno com aplicações, de Sheldon Ross- Ed: 8º - Capítulo 2.Problemas - Ex. 12
Uma escola fundamental oferece três cursos de línguas: um de espanhol, um de francês e outro de alemão. As classes estão abertas para todos os 100 estudantes da escola. Há 28 estudantes na classe de espanhol, 26 na classe de francês e 16 na classe de alemão. Há 12 estudantes que fazem aulas de espanhol e francês, 4 que fazem aulas de espanhol e alemão, e 6 que fazem aulas de francês e alemão. Além disso, há 2 estudantes fazendo os três cursos.
(a) Se um estudante é escolhido aleatoriamente, qual é a probabilidade de que ele ou ela não esteja matriculado(a) em nenhum dos cursos?
(b) Se um estudante é escolhido aleatoriamente, qual é a probabilidade de que ele ou ela esteja fazendo exatamente um curso de línguas?
(c) Se dois estudantes são escolhidos aleatoriamente, qual é a probabilidade de que pelo menos um deles esteja fazendo um curso de línguas?
Passo 1
E tome diagrama de venn. Essa ferramenta é muito poderosa pra auxiliar na resolução de problemas desse tipo.
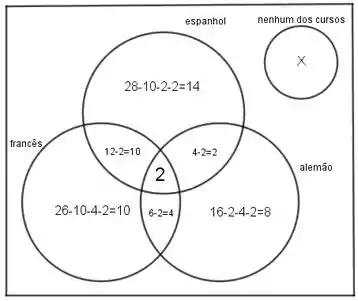
Passo 2
a. Vamos calcular quantos estudantes não estão matriculados em nenhum dos cursos “X”.
Como temos 100 estudantes no total. A probabilidade pedida é
Passo 3
b. Vamos encontrar quantos alunos fazem exatamente um curso de línguas.
De 100 estudantes, nossa resposta é, então:
Passo 4
c. Bom, vamos com calma nesse item para não errar bobagem:
Probabilidade é sempre o número de casos favoráveis (aquilo que o problema pede) sobre o número total de casos possíveis, não é mesmo?! o total de casos é o número de combinações em que eu posso escolher 2 alunos dentre os 100. O número de casos favoráveis ao qual o problema refere-se é escolher dois entre aqueles que fazem pelo menos um curso, ou seja, 2 de 50. Assim:
Resposta
a. 50%
b. 32%
c. 49/198