Estime os efeitos dos fatores. Baseado em um gráfico de probabilidade normal das estimativas dos efeitos. identifique um modelo para os dados desse experimento.
Conduza uma ANOVA, bascando-se no modelo identificado no item . Quais são suas conclusões?
Analise os resíduos e comente à adequação do modelo.
Encontre um modelo de regressão para prever o rendimento em termos dos nívceis reais dos fatores.
Esse planejamento pode ser Projetado em um plancjamento 2 com duas réplicas? Se afirmativo, esquematize o planejamento c mostre
a média e a faixa dos dois valores do rendimento em cada vértice do cubo. Discuta o valor prático desse gráfico.
Passo 1
Bom galera, para o experimento fatorial , temos a tabela:
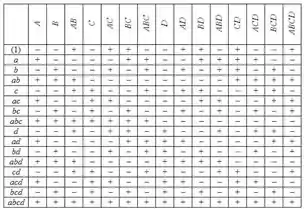
Estimando os efeitos dos fatores:
Fazendo igual para todos os outros fatores, temos:
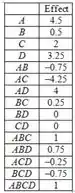
Passo 2
Belezinha, plotamos o gráfico de probabilidade normal dos efeitos estimados e temos:
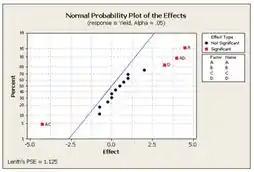
Examinando a magnitude dos efeitos e o mostra que os efeitos são significativos nos fatores , e nas interações e . Se for considerado significativo, então o fator também deve ser considerado como significativo. Portanto, os fatores , , e as interações e são significativos.
Passo 3
Agora, realizamos a analise das variâncias para isso vamos para as somas dos quadrados:
Fazendo o mesmo nos outros fatores, ficamos com:
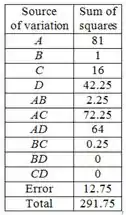
Passo 4
Cada por um fator ou interação tem grau de liberdade, tem graus de liberdade, tem graus de liberdade (a soma dos graus de liberdade das interações agrupadas). Encontrando cada como a razão de e correspondentes. Nosso resultado fica:
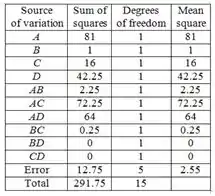
Encontrando o valor da estatística para cada fator e interação como uma razão de correspondente para . O resultado é:
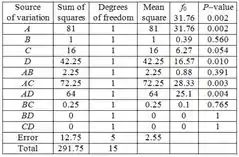
Buscamos fatores com valor pequeno, inferior a . Os fatores assim são , , e . Se for significativo, então também deve ser. De qualquer forma, o valor do teste de não é tão grande. Podemos concluir que os fatores significativos são , , , e .
Passo 5
Agora, para construir um modelo de regressão linear para os fatores , , , e . A constante é estimada pela média geral, e os coeficientes de regressão são estimados pela metade das estimativas do efeito correspondente. O modelo é:
E usaremos Minitab para construir o gráfico de probabilidade normal e os de resíduos:
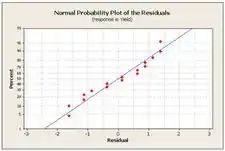
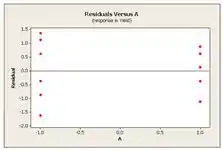
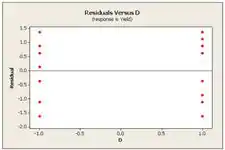
Os pontos no plot de probabilidade normal de resíduos ficam perto de uma linha reta. A suposição da normalidade parece estar satisfeita. Além disso, os lotes de resíduos versus valores e fatores ajustados mostram distribuição bastante simétrica dos pontos próximo de zero. A suposição de variâncias iguais está satisfeita. Concluímos que o modelo é adequado.
Passo 6
Então, usamos o Minitab para encontrar a equação de regressão, com os fatores significativos , , , e , encontraremos:
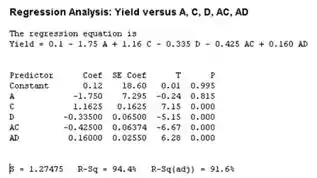
Logo, a equação de regressão fica:
Passo 7
Como existem três fatores principais significativos, temo um projeto fatorial . Os fatores de interesse são , e . Ficamos com:
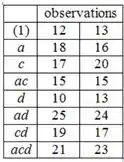
A tabela de médias e rendimento para cada corrida é:
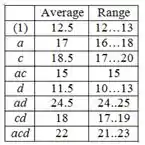
Então, o plot de design com médias é:
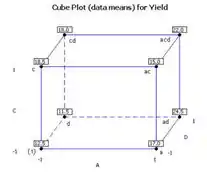
A partir disso, podemos ver que os grande valores dos fatores , e resutam em aumento do rendimento médio.
Resposta
Ei, a resposta está no passo a passo :)