Construa um gráfico de probabilidade normal das estimativas dos efeitos. Que efeitos parecem ser grandes?
Conduza uma análise de variância para confirmar às suas descobertas no item .
Plote os resíduos no papel de probabilidade normal, O gráfico é satisfatório?
Plote os resíduos contra os rendimentos previstos e contra cada um dos cinco fatores. Comente os eráficos.
Interprete qualquer interação significativa.
Quais são àas suas recomendações relativas às condições operacionais do processo?
Projete o planejamento deste Pproblema em um planejamento para nos fatores importantes, Esquematize o planejamento e mostre a média e a amplitude de rendimentos em cada corrida. Esse esquema ajuda na interpretação dos dados”?
Passo 1
Bom galera, vamos primeiro estimar os efeitos, para o experimento fatorial , temos a tabela:
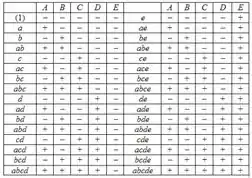
O sinal para cada interação pode ser obtido pela multiplicação dos sinais de fatores que estão nessa interação.
Passo 2
Belezinha, usando a tabela de sinais para calcular o efeito de . Adicionando os efeitos com os sinais correspondentes na coluna do fator considerado.
Todos os outros efeitos são encontrados da mesma forma. A tabela dos efeitos para todos os fatores e interação é dada por:
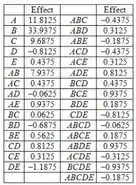
E o gráfico de probabilidade nomal de efeito é:
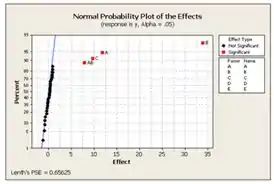
Examinando a magnitude dos efeitos e o gráfico de probabilidade normal dos efeitos mostra que os fatore , , e a interação são significativos. Realizando a analise de variancia:
Passo 3
Agora, calculando todas as outras somas de quadrados da mesma forma. O resultado está resumido na tabela:
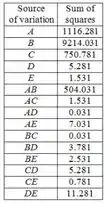
A soma total dos quadrados é:
E a soma dos quadrados para o erro:
Passo 4
Então, cada para um fator ou interação tem grau de liberdade, tem graus de liberdade. Encontrando cada como a razão de e correspondentes. O resultado é:
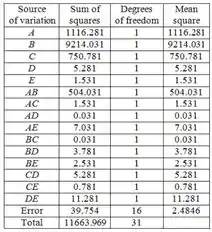
Passo 5
Agora, encontramos o valor estatístico para cada fator e interação como uma razão correspondente para . O resultado fica:
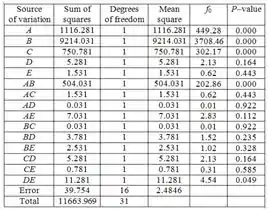
Procuramos fatores com valores pequenos. Tais fatores são , , e a interação . Este resultado concorda com a análise dos efeitos dos fatores. Portanto, o principal efeito dos fatores , , e a interação deve ser considerado significativo.
Passo 6
Então, construímos um modelo de regressão linar para os fatores , , e a interação . A constante é estimada pela média geral, e os coeficientes de regressão são estimados pela metade das estimativas de efeito correspondente. O modelo fica:
Usamos o Minitab para construir o gráfico de probabilidade normal. O gráfico de probabilidade normal é:
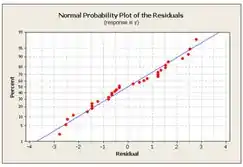
Os pontos no gráfico estão perto da linha. Podemos concluir que não há desvios da normalidade. E os gráficos de resíduos são:
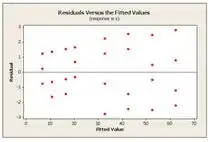


As parcelas residuais versus os valores e fatores ajustados , e mostram distribuição bastante simétrica dos pontos próximos de zero. Portanto, podemos concluir que o modelo de regressão encontrado acima é adequado. Observe que os pontos nas parcelas residuais versus os fatores e que não estão incluídos no modelo não são simétricos sobre zero.
Passo 7
A única interação significativa é a ,a interação da configuração de abertura e do tempo de exposição. Uma vez que os efeitos de , e são positivos, deve-se, antes de tudo, utilizar os fatores e em seus altos valores para aumentar o rendimento. O efeito de interação só funcionará no aumento do rendimento.
Como todos os fatores significativos tem efeitos positivos, para aumentar o rendimento desse-se utilizar os fatores , , e seus valores elevados.
Passo 8
Por fim, projetar o desenho fatorial para os fatores , e . Os dados são:
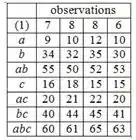
O plot do design com médias é:
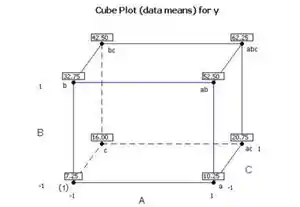
A partir disso podemos ver que os alto valores dos fatores , e resultam em aumento do rendimento médio.
Resposta
Ei, a resposta está no passo a passo :)