Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 14.Exercícios - Ex. 18
Estime os efeitos e prepare um gráfico normal dos efeitos.
Construa uma tabela de análise de variância, basenado-se no modelo tentativa identificado em .
Construa um gráfico de probabilidade normal dos resíduos e comente os resultados..
Passo 1
Bom galera, para o experimento fatorial , temos a tabela:
Estimando os efeitos dos fatores:
Fazemos igual em todos os outros fatores:
Passo 2
Belezinha, agora plotamos o gráfico de probabilidade normal dos efeitos pelo Minitab:
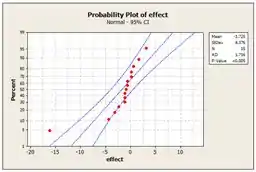
Dessa plotagem, o principal efeito e a interação são significativos, pois esses pontos longe da linha, passam pelos outros pontos.
Passo 3
Agora, usamos a fórmula para a soma dos quadrados:
Aplicando a formula ficamos com:
Da mesma forma encontramos:
E a tabela ANOVA é:
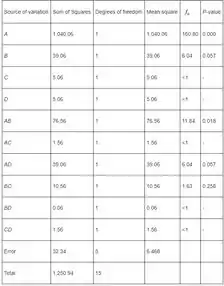
Passo 4
Os resíduos do experimento é obtido pelo modelo de regressão:
Onde a interseção é a média geral de todas as observações e é o efeito médio estimado para e é o efeito médio estimado para .
Os valores previstos e os resíduos são:
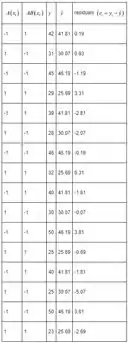
Plotando o gráfico de probabilidade dos resíduos:
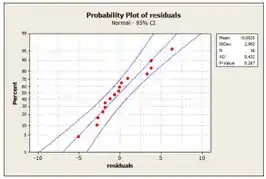
Nisso, os resíduos estão aproximadamente ao longo da linha reta. Portanto, não há nenhum problema com a normalidade dos dados.
Resposta
Ei, a resposta está no passo a passo :)