Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 2.Exercícios propostos - Ex. 1
Estudar a distribuição formada pela diferença entre os pontos obtidos (em módulo) quando jogamos dois dados. Calcula a média e o desvio padrão dessa distribuição.
Passo 1
Olá galerinha, tudo bem com vocês? Vamos começar relembrando algumas teoriazinhas? Então vamos lá!
Uma variável aleatória é sempre associada a seus resultados mutuamente exclusivos a probabilidade. E a variável aleatória é dita discreta quando pode assumir um número finito de valores dentro de um intervalo finito.
A distribuição de probabilidades é uma série de eventos mutuamente exclusivos que constituem a totalidade dos resultados numa experiência aleatória, isto é:
A cada evento , associamos um número real , e teremos como consequência que:
Um conjunto de valores de , correspondentes à probabilidade de ocorrer , que somados igualam a unidade, constitui uma distribuição de probabilidades.
Passo 2
Então, vamos lá para o nosso exercício. Sabemos que um dado tem número de 1 a 6, e pelo enunciado também sabemos que vamos jogar dois dados e calcular a diferença dos pontos obtidos em módulo (relembrando que módulo sempre será um número positivo).
Então vamos considerar o seguinte:
- 1° dado;
- 2° dado.
Vamos criar uma tabela, onde iremos fazer e :
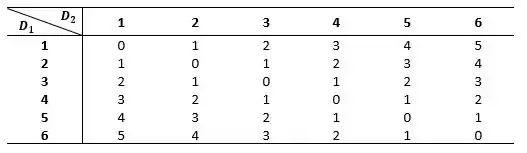
A média de distribuição (), da variável , é a soma dos produtos dos valores da variável pelas respectivas probabilidades, isto é:
E o desvio padrão pela seguinte equação:
Passo 3
Como temos 2 dados, temos: . Então iremos calcular o valor de para cada :
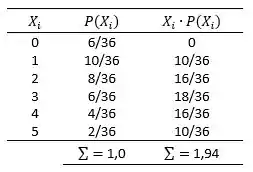
Então a média de distribuição é:
Com o valor da média conseguimos calcular o desvio padrão:
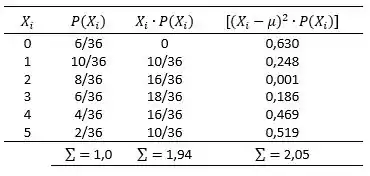
Então:
Tchau pessoal!
Resposta
;
.